如图所示,一根内壁光滑的直角三角形玻璃管子处于竖直平面内,倾斜角为θ= 37°,让两个小球分别从顶点A由静止开始出发,一个球沿AC滑下,到达C所用的时间为t1,另一个球竖直自由下落经过B到达C,所用的时间为t2,在转弯处有个极小的光滑圆弧,可确保小球转弯时无机械能损失,且转弯时间可以忽略不计。问: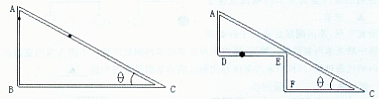
(1)计算t1∶ t2的值;
(2)若用同样的玻璃管把ABC轨道改为如图所示的ADEFC(在转弯处均有个极小的光滑圆弧),仍让小球从A静止开始运动,依次通过D、E、F后到达C点所用时间为t3,试定性说明t3和t1、t2的大小关系。








 粤公网安备 44130202000953号
粤公网安备 44130202000953号