如图所示，倾斜轨道AB的倾角为37^o，CD、EF轨道水平，AB与CD通过光滑圆弧管道BC连接，CD右端与竖直光滑圆周轨道相连。小球可以从D进入该轨道，沿轨道内侧运动，从E滑出该轨道进入EF水平轨道。小球由静止从A点释放，已知AB长为5R，CD长为R，重力加速度为g，小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5，sin37^o=0.6，cos37^o=0.8，圆弧管道BC入口B与出口C的高度差为1.8R。求：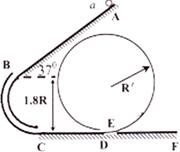

⑴小球滑到斜面底端C时速度的大小。
(2)小球对刚到C时对轨道的作用力。
(3)要使小球在运动过程中不脱离轨道，竖直圆周轨道的半径R’应该满足什么条件？若R’=2.5R，小球最后所停位置距D（或E）多远？
注：在运算中，根号中的数值无需算出。