已知 是两条不同直线,
是两条不同直线, 、β、γ是三个不同平面.下列命题中正确的是 .
、β、γ是三个不同平面.下列命题中正确的是 .
(1).若 ⊥γ,β⊥γ,则
⊥γ,β⊥γ,则 //β
//β
(2).若 ⊥
⊥ ,
,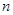 ⊥
⊥ ,则
,则 //
//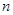
(3).若 //
// ,
,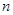 //
// ,则
,则 //
//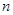
(4).若 //
// ,
, //β,则
//β,则 //β
//β
已知 是不同的直线,
是不同的直线,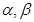 是不同的平面,有下列命题:
是不同的平面,有下列命题:
①若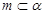 ,
, ∥
∥ ,则
,则 ∥
∥ ;
;
②若 ∥
∥ ,
, ∥
∥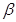 ,则
,则 ∥
∥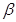 ;
;
③若 ,
, ∥
∥ ,则
,则 ∥
∥ 且
且 ∥
∥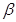 ;
;
④若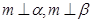 ,则
,则 ∥
∥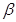 .
.
其中正确的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
试题篮
()