初中数学二次函数的应用试题

随着新农村的建设和旧城的改造，我们的家园越来越美丽，小明家附近广场中央新修了个圆形喷水池，在水池中心竖直安装了一根高为2米的喷水管，它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高，水柱落地处离池中心3米．

（1）请你建立适当的平面直角坐标系，并求出水柱抛物线的函数解析式；

（2）求出水柱的最大高度是多少？

某食品连锁店研制出一种新式月饼，每块成本为6元．试销一段时间后发现，若每块月饼的售价不超过10元，每天可销售300块；若每块月饼的售价超过10元，每提高1元，每天的销量就会减少30块．这家食品连锁店每天需要支付因生产这种月饼而产生的其他费用（不含月饼成本）200元．设每块月饼的售价为 $x$（元 $)$，食品连锁店每天销售这种月饼的纯收入为 $y$（元 $)$．（注：纯收入 $=$销售额 $-$成本 $-$其他费用）

（1）当每块月饼售价不超过10元时，请直接写出 $y$与 $x$之间的函数关系式：　．当每块月饼售价超过10元时，请直接写出 $y$与 $x$之间的函数关系式：　　；

（2）如果这种月饼每块的售价不超过12元，那么如何定价才能使该食品连锁店每天销售这种月饼的纯收入提高？最高纯收入为多少元？

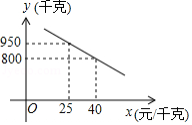
某商场经营一种海产品，进价是每千克20元，根据市场调查发现，每日的销售量 $y$（千克）与售价 $x$（元 $/$千克）是一次函数关系，如图所示：

（1）求 $y$与 $x$的函数关系式（不求自变量取值范围）；

（2）某日该商场出售这种海产品获得了21000元的利润，该海产品的售价是多少？

（3）若某日该商场这种海产品的销售量不少于650千克，该商场销售这种海产品获得的最大利润是多少？

某商店以每件50元的价格购进一批新型产品，如果按每件60元出售，那么每周可销售500件．根据市场规律，这种产品的销售单价每提高1元，其销售量每周相应减少10件，但每件产品的销售单价不低于60元，且不能高于85元，设每周的销售量为 $y$（件 $)$，这种产品的销售单价为 $x$（元 $)$，解答下列问题：

（1）请直接写出 $y$与 $x$之间的函数关系式；

（2）商家要想每周获得8000元的销售利润，销售单价应定为多少元？

（3）销售单价为多少元时，每周获得的销售利润最大？最大利润是多少元？

某商店购进一批进价为20元 $/$件的日用商品，第一个月，按进价提高 $50\%$的价格出售，售出400件，第二个月，商店准备在不低于原售价的基础上进行加价销售，根据销售经验，提高销售单价会导致销售量的减少．销售量 $y$（件 $)$与销售单价 $x$（元 $)$的关系如图所示．

（1）图中点 $P$所表示的实际意义是　　；销售单价每提高1元时，销售量相应减少　　件；

（2）请直接写出 $y$与 $x$之间的函数表达式　　；自变量 $x$的取值范围为　　；

（3）第二个月的销售单价定为多少元时，可获得最大利润？最大利润是多少？

某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量 $y$（本 $)$与每本纪念册的售价 $x$（元 $)$之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．

（1）请直接写出 $y$与 $x$的函数关系式；

（2）当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？

（3）设该文具店每周销售这种纪念册所获得的利润为 $w$元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？

有一家苗圃计划植桃树和柏树，根据市场调查与预测，种植桃树的利润 $y_1$（万元）与投资成本 $x$（万元）满足如图①所示的二次函数 $y_1=a{x}^2$；种植柏树的利润 $y_2$（万元）与投资成本 $x$（万元）满足如图②所示的正比例函数 $y_2=\mathit{kx}$．

（1）分别求出利润 $y_1$（万元）和利润 $y_2$（万元）关于投资成本 $x$（万元）的函数关系式；

（2）如果这家苗圃以10万元资金投入种植桃树和柏树，桃树的投资成本不低于2万元且不高于8万元，苗圃至少获得多少利润？最多能获得多少利润？

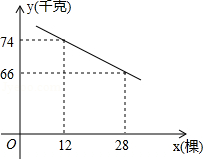
某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果 $y$（千克），增种果树 $x$（棵 $)$，它们之间的函数关系如图所示．

（1）求 $y$与 $x$之间的函数关系式；

（2）在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实6750千克？

（3）当增种果树多少棵时，果园的总产量 $w$（千克）最大？最大产量是多少？

如图1， $\mathit{\Delta ABC}$中， $\angle C=90°$，线段 $\mathit{DE}$在射线 $\mathit{BC}$上，且 $\mathit{DE}=\mathit{AC}$，线段 $\mathit{DE}$沿射线 $\mathit{BC}$运动，开始时，点 $D$与点 $B$重合，点 $D$到达点 $C$时运动停止，过点 $D$作 $\mathit{DF}=\mathit{DB}$，与射线 $\mathit{BA}$相交于点 $F$，过点 $E$作 $\mathit{BC}$的垂线，与射线 $\mathit{BA}$相交于点 $G$．设 $\mathit{BD}=x$，四边形 $\mathit{DEGF}$与 $\mathit{\Delta ABC}$重叠部分的面积为 $S$， $S$关于 $x$的函数图象如图2所示（其中 $0<x⩽1$， $1<x⩽m$， $m<x⩽3$时，函数的解析式不同）

（1）填空： $\mathit{BC}$的长是　　；

（2）求 $S$关于 $x$的函数关系式，并写出 $x$的取值范围．

为备战2016年里约奥运会，中国女排的姑娘们刻苦训练，为国争光，如图，已知排球场的长度 $\mathit{OD}$为18米，位于球场中线处球网的高度 $\mathit{AB}$为2.43米，一队员站在点 $O$处发球，排球从点 $O$的正上方1.8米的 $C$点向正前方飞出，当排球运行至离点 $O$的水平距离 $\mathit{OE}$为7米时，到达最高点 $G$建立如图所示的平面直角坐标系．

（1）当球上升的最大高度为3.2米时，求排球飞行的高度 $y$（单位：米）与水平距离 $x$（单位：米）的函数关系式．（不要求写自变量 $x$的取值范围）．

（2）在（1）的条件下，对方距球网0.5米的点 $F$处有一队员，他起跳后的最大高度为3.1米，问这次她是否可以拦网成功？请通过计算说明．

（3）若队员发球既要过球网，又不出边界，问排球飞行的最大高度 $h$的取值范围是多少？（排球压线属于没出界）

某公司研发了一款成本为60元的保温饭盒，投放市场进行试销售，按物价部门规定，其销售单价不低于成本，但销售利润不高于 $65\%$，市场调研发现，保温饭盒每天的销售数量 $y$（个 $)$与销售单价 $x$（元 $)$满足一次函数关系；当销售单价为70元时，销售数量为160个；当销售单价为80元时，销售数量为140个（利润率 $=\frac{\mathit{利润}}{\mathit{成本}}\times 100\backslash \%)$

（1）求 $y$与 $x$之间的函数关系式；

（2）当销售单价定为多少元时，公司每天获得利润最大，最大利润为多少元？

夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务．为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．

（1）设第 $x$天生产空调 $y$台，直接写出 $y$与 $x$之间的函数解析式，并写出自变量 $x$的取值范围．

（2）若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第 $x$天的利润为 $W$元，试求 $W$与 $x$之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．

如图，直线 $l$的解析式为 $y=-x+4$，它与 $x$轴和 $y$轴分别相交于 $A$， $B$两点．平行于直线 $l$的直线 $m$从原点 $O$出发，沿 $x$轴的正方向以每秒1个单位长度的速度运动．它与 $x$轴和 $y$轴分别相交于 $C$， $D$两点，运动时间为 $t$秒 $(0⩽t⩽4)$，以 $\mathit{CD}$为斜边作等腰直角三角形 $\mathit{CDE}(E$， $O$两点分别在 $\mathit{CD}$两侧）．若 $\mathit{\Delta CDE}$和 $\mathit{\Delta OAB}$的重合部分的面积为 $S$，则 $S$与 $t$之间的函数关系的图象大致是 $($　　 $)$

A．B．

C．D．

铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀．小张购进一批食材制作特色美食，每盒售价为50元，由于食材需要冷藏保存，导致成本逐日增加，第 $x$天 $(1⩽x⩽15$且 $x$为整数）时每盒成本为 $p$元，已知 $p$与 $x$之间满足一次函数关系；第3天时，每盒成本为21元；第7天时，每盒成本为25元，每天的销售量为 $y$盒， $y$与 $x$之间的关系如下表所示：

第 $x$天	$1⩽x⩽6$	$6<x⩽15$
每天的销售量 $y/$盒	10	$x+6$

（1）求 $p$与 $x$的函数关系式；

（2）若每天的销售利润为 $w$元，求 $w$与 $x$的函数关系式，并求出第几天时当天的销售利润最大，最大销售利润是多少元？

（3）在“荷花美食”厨艺秀期间，共有多少天小张每天的销售利润不低于325元？请直接写出结果．

某商场购进一批单价为20元的日用商品，如果以单价30元销售，那么半月内可销售出400件，根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高1元，销售量相应减少20件，当销售量单价是　　元 $/$件，才能在半月内获得最大利润．