某电商销售一款夏季时装,进价40元 件,售价110元 件,每天销售20件,每销售一件需缴纳电商平台推广费用 元 .未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数 为正整数)的增大而增大, 的取值范围应为 .
某宾馆拥有客房100间,经营中发现:每天入住的客房数 (间)与其价格 (元) 满足一次函数关系,部分对应值如表:
(元) |
180 |
260 |
280 |
300 |
(间) |
100 |
60 |
50 |
40 |
(1)求 与 之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润 当日房费收入 当日支出)
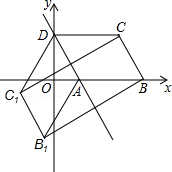
如图,已知 的三个顶点 、 、 , ,作 关于直线 的对称图形
(1)若 ,试求四边形 面积 的最大值;
(2)若点 恰好落在 轴上,试求 的值.
某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过 人时,每增加1人,人均收费降低1元;超过 人时,人均收费都按照 人时的标准.设景点接待有 名游客的某团队,收取总费用为 元.
(1)求 关于 的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求 的取值范围.
图中是抛物线拱桥, 处有一照明灯,水面 宽 ,从 、 两处观测 处,仰角分别为 、 ,且 , ,以 为原点, 所在直线为 轴建立直角坐标系.
(1)求点 的坐标;
(2)水面上升 ,水面宽多少 取1.41,结果精确到 ?

2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价 (元 与月份 ,且 为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本 (元 与月份 ,且 为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份 |
|
3 |
4 |
5 |
6 |
|
售价 元 |
|
12 |
14 |
16 |
18 |
|
(1)求 与 之间的函数关系式.
(2)求 与 之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为 (元 ,求 与 之间的函数关系式,哪个月份销售每千克猪肉所获得的利润最大?最大利润是多少元?

我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量 (千克)与销售单价 (元 符合一次函数关系,如图所示.
(1)求 与 之间的函数关系式,并写出自变量 的取值范围;
(2)若在销售过程中每天还要支付其他费用450元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?

某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于 ,市场调研发现,在一段时间内,每天销售数量 (个 与销售单价 (元 符合一次函数关系,如图所示:
(1)根据图象,直接写出 与 的函数关系式.
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?

某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的 .在销售过程中发现,这种儿童玩具每天的销售量 (件 与销售单价 (元 满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.
(1)求 与 之间的函数关系式.
(2)当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少?
某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为 元,平均月销售量为 件.
(1)求出 与 的函数关系式,并写出自变量 的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量 与销售单价 (元 满足如图所示的函数关系(其中 .
(1)直接写出 与 之间的函数关系式及自变量的取值范围.
(2)若农贸公司每天销售该特产的利润要达到3100元,则销售单价 应定为多少元?
(3)设每天销售该特产的利润为 元,若 ,求:销售单价 为多少元时,每天的销售利润最大?最大利润是多少元?

某工厂生产一种火爆的网红电子产品,每件产品成本16元、工厂将该产品进行网络批发,批发单价 (元 与一次性批发量 (件 为正整数)之间满足如图所示的函数关系.
(1)直接写出 与 之间所满足的函数关系式,并写出自变量 的取值范围;
(2)若一次性批发量不超过60件,当批发量为多少件时,工厂获利最大?最大利润是多少?

某商场销售一种商品的进价为每件30元,销售过程中发现月销售量 (件 与销售单价 (元 之间的关系如图所示.
(1)根据图象直接写出 与 之间的函数关系式.
(2)设这种商品月利润为 (元 ,求 与 之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?

某商场销售一种商品的进价为每件30元,销售过程中发现月销售量 (件 与销售单价 (元 之间的关系如图所示.
(1)根据图象直接写出 与 之间的函数关系式.
(2)设这种商品月利润为 (元 ,求 与 之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
试题篮
()