我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在 中, 是 边上的中线, 与 的“极化值”就等于 的值,可记为 △ .
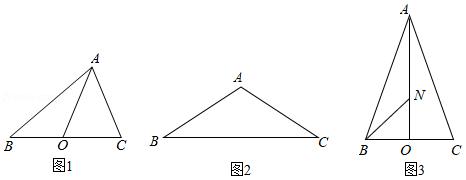
(1)在图1中,若 , , , 是 边上的中线,则 △ , △ ;
(2)如图2,在 中, , ,求 △ 、 △ 的值;
(3)如图3,在 中, , 是 边上的中线,点 在 上,且 .已知 △ , △ ,求 的面积.
如图, 中, , , ,点 是 的中点,将 沿 翻折得到 ,连 ,则线段 的长等于

A.2B. C. D.
如图,在 中, , ,点 、 分别在 、 上,且 ,将 沿 所在直线折叠得到△ (点 在四边形 内),连接 ,则 的长为 .

如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以 为圆心, 为半径画圆,选取的格点中除点 外恰好有3个在圆内,则 的取值范围为
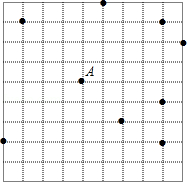
A. B. C. D.
如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为 、 、 ;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为 、 、 .其中 , , , ,则

A.86B.64C.54D.48
思维启迪:
(1)如图1, , 两点分别位于一个池塘的两端,小亮想用绳子测量 , 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达 点的点 ,连接 ,取 的中点 (点 可以直接到达 点),利用工具过点 作 交 的延长线于点 ,此时测得 米,那么 , 间的距离是 200 米.
思维探索:
(2)在 和 中, , ,且 , ,将 绕点 顺时针方向旋转,把点 在 边上时 的位置作为起始位置(此时点 和点 位于 的两侧),设旋转角为 ,连接 ,点 是线段 的中点,连接 , .
①如图2,当 在起始位置时,猜想: 与 的数量关系和位置关系分别是 ;
②如图3,当 时,点 落在 边上,请判断 与 的数量关系和位置关系,并证明你的结论;
③当 时,若 , ,请直接写出 的值.

如图,在 的纸片中, , , .点 在边 上,以 为折痕将 折叠得到 , 与边 交于点 .若 为直角三角形,则 的长是 .

如图,在矩形 中, , ,将矩形 折叠,使点 与点 重合,折痕为 .给出以下四个结论:① ;② 是等边三角形;③ ;④ .其中正确的结论序号是 .

试题篮
()