初中数学勾股定理试题

如图，△ ABC中， AC＝ BC＝3， AB＝2，将它沿 AB翻折得到△ ABD，点 P、 E、 F分别为线段 AB、 AD、 DB上的动点，则 PE+ PF的最小值是（　　）

A．

$\frac{\sqrt{10}}{3}$

B．

$\frac{2\sqrt{2}}{3}$

C．

$\frac{4\sqrt{2}}{3}$

D．

$\frac{8\sqrt{10}}{3}$

腰长为5，高为4的等腰三角形的底边长为 　　．

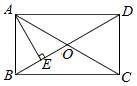
如图，在矩形 ABCD中， AD＝8，对角线 AC与 BD相交于点 O， AE⊥ BD，垂足为点 E，且 AE平分∠ BAC，则 AB的长为 　　．

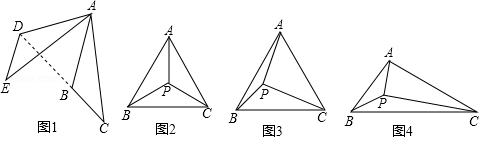
（1）【操作发现】

如图1，将△ ABC绕点 A顺时针旋转60°，得到△ ADE，连接 BD，则∠ ABD＝ 　　度．

（2）【类比探究】

如图2，在等边三角形 ABC内任取一点 P，连接 PA， PB， PC，求证：以 PA， PB， PC的长为三边必能组成三角形．

（3）【解决问题】

如图3，在边长为 $\sqrt{7}$ 的等边三角形 ABC内有一点 P，∠ APC＝90°，∠ BPC＝120°，求△ APC的面积．

（4）【拓展应用】

如图4是 A， B， C三个村子位置的平面图，经测量 AC＝4， BC＝5，∠ ACB＝30°， P为△ ABC内的一个动点，连接 PA， PB， PC．求 PA+ PB+ PC的最小值．

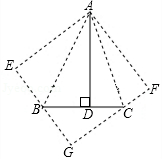
如图，在△ ABC中，∠ BAC＝45°， AD⊥ BC于点 D， BD＝6， DC＝4，求 AD的长．小明同学利用翻折，巧妙地解答了此题，按小明的思路探究并解答下列问题：

（1）分别以 AB， AC所在直线为对称轴，画出△ ABD和△ ACD的对称图形，点 D的对称点分别为点 E， F，延长 EB和 FC相交于点 G，求证：四边形 AEGF是正方形；

（2）设 AD＝ x，建立关于 x的方程模型，求出 AD的长．

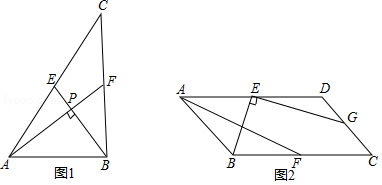
如图1， AF， BE是△ ABC的中线， AF⊥ BE，垂足为点 P，设 BC＝ a， AC＝ b， AB＝ c，则 a ²+ b ²＝5 c ²，利用这一性质计算．如图2，在▱ ABCD中， E， F， G分别是 AD， BC， CD的中点， EB⊥ EG于点 E， AD＝8， AB＝2 $\sqrt{5}$ ，则 AF＝ 　　．

如图，在四边形ABCD中， $\angle \mathit{ABC}＝90°$， $\mathit{AB}＝3$， $\mathit{BC}＝4$， $\mathit{CD}＝10$， $\mathit{DA}=5\sqrt{5}$，则BD的长为　   　．

如图，在▱ABCD中， $\mathit{AB}=2\sqrt{13}\text{cm}$， $\mathit{AD}＝4\mathit{cm}，$ $\mathit{AC}\perp \mathit{BC}$，则△DBC比△ABC的周长长　　cm．

如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（　　）

A．2B． $\frac{2\sqrt{5}}{5}$C． $\frac{1}{2}$D． $\frac{\sqrt{5}}{5}$

如图，△ABC中，AB＝AC，AD是∠BAC的平分线．已知AB＝5，AD＝3，则BC的长为（　　）

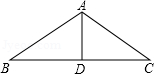
A．5B．6C．8D．10

如图，AB＝6，O是AB的中点，直线l经过点O，∠1＝120°，P是直线l上一点，当△APB为直角三角形时，AP＝　    　．

已知，如图，△ ACB和△ ECD都是等腰直角三角形，∠ ACB＝∠ ECD＝90°， D为 AB边上一点．

（1）求证：△ ACE≌△ BCD；

（2）求证：2 CD ²＝ AD ²+ DB ²．

如图， CD为⊙ O的直径，弦 AB⊥ CD，垂足为 M，若 AB＝12， OM： MD＝5：8，则⊙ O的周长为（　　）

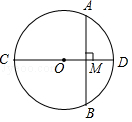
A．

26π

B．

13π

C．

$\frac{96\pi }{5}$

D．

$\frac{39\sqrt{10}\pi }{5}$

如图，将半圆形纸片折叠，使折痕 CD与直径 AB平行， $\stackrel{⏜}{\mathit{CD}}$ 的中点 P落在 OP上的点 P'处，且 OP'＝ $\frac{1}{3}$ OP，折痕 CD＝2 $\sqrt{3}$ ，则tan∠ COP的值为（　　）

A．

$\frac{6}{5}\sqrt{5}$

B．

$\frac{\sqrt{3}}{2}$

C．

$\frac{\sqrt{5}}{2}$

D．

$\frac{2}{5}\sqrt{5}$

如图，在正方形 ABCD中，点 E， F分别在 BC， CD上，如果 AE＝3， EF＝2， AF＝ $\sqrt{\text{13}}$ ，那么正方形 ABCD的边长等于 　．