初中数学相似多边形的性质试题

如图，在正方形网格上，若使△ABC∽△PBD，则点P应在(     )

A．P1处

B．P2处

C．P3处

D．P4处

如图，△ABC中，∠B=900，AB=6，BC=8，将△ABC沿DE折叠，使点C落在AB边上的C´处，并且C´D∥BC，则CD的长是(    )

A．

B．

C．

D．

如图所示，图中共有相似三角形(     )

A．2对

B．3对

C．4对

D．5对

如图，小芳和爸爸正在散步，爸爸身高1.8m，他在地面上的影长为2.1m．若小芳比爸爸矮0.3m，则她的影长为（  ）．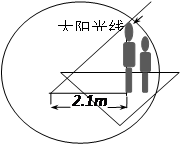

A．1.3m

B．1.65m

C．1.75m

D．1.8m

如图，在中，，，把边长分别为的个正方形依次放入中，请回答下列问题：

（1）按要求填表

	1	2	3

（2）第个正方形的边长       ；
（3）若是正整数，且，试判断的关系．

如图，把菱形ABCD沿着BD的方向平移到菱形A/B/C/D/′的位置，

(1)求证：重叠部分的四边形B/EDF/是菱形
(2)若重叠部分的四边形B/EDF/面积是把菱形ABCD面积的一半,且BD=，求则此菱形移动的距离．

如图，已知⊙O的弦CD垂直于直径AB，点E在CD上，且EC =" EB" .

（1）求证：△CEB∽△CBD ；
（2）若CE = 3，CB="5" ，求DE的长.

在和中，，，．

（1）判断这两个三角形是否相似？并说明为什么？
（2）能否分别过在这两个三角形中各作一条辅助线，使分割成的两个三角形与分割成的两个三角形分别对应相似？证明你的结论．

如图，图中的小方格都是边长为1的正方形， △ABC与△A′ B′ C′是关于点0为位似中心的位似图形，它们的顶点都在小正方形的顶点上．

(1)画出位似中心点0；
(2)求出△ABC与△A′B′C′的位似比；
(3)以点0为位似中心，再画一个△A1B1C1，使它与△ABC的位似比等于1.5．

某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图).则小鱼上的点(a,b)对应大鱼上的点是____________________.

如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆．小丽站在离南岸边15米的点P处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，则河宽为        米．

如图，矩形ABCD中，AE⊥BD于E，若BE=4，DE=9,则矩形的面积是______________.

在平面直角坐标系中，已知A(6，3)、B(10，0)两点，以坐标原点O为位似中心，相似比为，把线段AB缩小后得到线段A/B/，则A/B/的长度等于____________．

如图，在Ｒt△ABC中,∠C=90°,点D是AB边上的一定点,点E是AC上的一个动点,若再增加一个条件就能使△ADE与△ABC相似,则这个条件可以是________________________.

有一张比例尺为1∶4000的地图上，一块多边形地区的周长是60cm，面积是250cm2，则这个地
区的实际周长_________m，面积是___________m2