初中数学相似三角形的应用试题

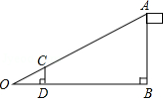
在平面直角坐标系中，已知抛物线经过点和点，关于原点对称的抛物线为．

（1）求抛物线的表达式；

（2）点在抛物线上，且位于第一象限，过点作轴，垂足为．若与相似，求符合条件的点的坐标．

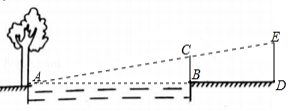
周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时，他们选择了河对岸岸边的一棵大树，将其底部作为点，在他们所在的岸边选择了点，使得与河岸垂直，并在点竖起标杆，再在的延长线上选择点，竖起标杆，使得点与点、共线．

已知：，，测得，，．测量示意图如图所示．请根据相关测量信息，求河宽．

某市为了打造森林城市，树立城市新地标，实现绿色、共享发展理念，在城南建起了"望月阁"及环阁公园．小亮、小芳等同学想用一些测量工具和所学的几何知识测量"望月阁"的高度，来检验自己掌握知识和运用知识的能力．他们经过观察发现，观测点与"望月阁"底部间的距离不易测得，因此经过研究需要两次测量，于是他们首先用平面镜进行测量．方法如下：如图，小芳在小亮和"望月阁"之间的直线 $\mathit{BM}$ 上平放一平面镜，在镜面上做了一个标记，这个标记在直线 $\mathit{BM}$ 上的对应位置为点 $C$ ，镜子不动，小亮看着镜面上的标记，他来回走动，走到点 $D$ 时，看到"望月阁"顶端点 $A$ 在镜面中的像与镜面上的标记重合，这时，测得小亮眼睛与地面的高度 $\mathit{ED}=1.5$ 米， $\mathit{CD}=2$ 米，然后，在阳光下，他们用测影长的方法进行了第二次测量，方法如下：如图，小亮从 $D$ 点沿 $\mathit{DM}$ 方向走了16米，到达"望月阁"影子的末端 $F$ 点处，此时，测得小亮身高 $\mathit{FG}$ 的影长 $\mathit{FH}=2.5$ 米， $\mathit{FG}=1.65$ 米．

如图，已知 $\mathit{AB}\perp \mathit{BM}$ ， $\mathit{ED}\perp \mathit{BM}$ ， $\mathit{GF}\perp \mathit{BM}$ ，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出"望月阁"的高 $\mathit{AB}$ 的长度．

如图，在横格作业纸（横线等距）上画一条直线，与横格线交于 $A$ ， $B$ ， $C$ 三点，则 $\mathit{BC}:\mathit{AC}$ 等于 $($ 　　 $)$

A．

$2:3$

B．

$2:5$

C．

$3:4$

D．

$3:5$

在某一时刻，测得一根高为的竹竿的影长为，同时同地测得一栋楼的影长为，则这栋楼的高度为　　．

如图是测量河宽的示意图，与相交于点，，测得，，，求得河宽　　．

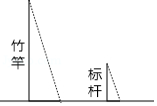
《孙子算经》是中国古代重要的数学著作， 成书于约一千五百年前， 其中有首歌谣： 今有竿不知其长， 量得影长一丈五尺， 立一标杆， 长一尺五寸， 影长五寸， 问竿长几何？意即： 有一根竹竿不知道有多长， 量出它在太阳下的影子长一丈五尺， 同时立一根一尺五寸的小标杆， 它的影长五寸 （提 示： 1 丈 $=10$ 尺， 1 尺 $=10$ 寸） ，则竹竿的长为 $($ 　　 $)$

A．	A ． 五丈B ． 四丈五尺C ． 一丈D ． 五尺

如图，数学活动小组为了测量学校旗杆的高度，使用长为的竹竿作为测量工具．移动竹竿，使竹竿顶端的影子与旗杆顶端的影子在地面处重合，测得，，则旗杆的高为　　．

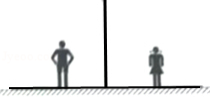
如图，小军、小珠之间的距离为 $2.7m$ ，他们在同一盏路灯下的影长分别为 $1.8m$ ， $1.5m$ ，已知小军、小珠的身高分别为 $1.8m$ ， $1.5m$ ，则路灯的高为 　　 $m$ ．

如图，利用标杆BE测量建筑物的高度，标杆BE高1．5m，测得AB=2m，BC=14cm，则楼高CD为        m．

有一块两条直角边BC、AC的长分别为3厘米和4厘米的Rt△ABC的铁片，现要把它加工成一个面积尽最大的正方形，甲、乙两位师傅加工方案分别如图所示，请用你学过的知识说明哪位师傅的加工方案符合要求（加工中的损耗忽略不计）．

如图，小明把手臂水平向前伸直，手持小尺竖直，瞄准小尺的两端E、F，不断调整站立的位置，使在点D处恰好能看到铁塔的顶部B和底部A，设小明的手臂长，小尺长，点D到铁塔底部的距离AD=，则铁塔的高度是__________．

如图，在钝角三角形ABC中，AB＝6cm，AC＝12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是（  ）

A.3秒或4.8秒
B.3秒
C.4.5秒
D.4.5秒或4.8秒

如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF，tanα=，则“人字梯”的顶端离地面的高度AD是（    ）

A．144cm

B．180cm

C．240cm

D．360cm

（年新疆、生产建设兵团）如图，李明打网球时，球恰好打过网，且落在离网4m的位置上，则网球的击球的高度h为          ．