高中数学充分条件、必要条件、充要条件填空题

“a＝1”是“函数f(x)＝x＋acosx在区间上为增函数”的     条件（在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中，选择适当的一种填空）．

“a＝1”是“函数f(x)＝x＋acosx在区间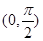上为增函数”的     条件（在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中，选择适当的一种填空）．

若a、b为实数，则“0<ab<1”是“b<”的________条件．

下列四个结论正确的是________．(填序号)
①“x≠0”是“x＋|x|>0”的必要不充分条件；
②已知a、b∈R，则“|a＋b|＝|a|＋|b|”的充要条件是ab>0；
③“a>0，且Δ＝b²－4ac≤0”是“一元二次不等式ax²＋bx＋c≥0的解集是R”的充要条件；
④“x≠1”是“x²≠1”的充分不必要条件．

设a>0且a≠1，则“函数f(x)＝a^x在R上是减函数”是“函数g(x)＝(2－a)x³在R上是增函数”的__________条件．

“a≤0”是“函数f(x)＝|(ax－1)x|在区间是(0，＋∞)内单调递增”的________条件．

“函数g(x)=(2-a)在区间(0,+∞)上是增函数”的充分不必要条件是a∈　                 .

在△ABC中，角A，B，C所对的边分别为a，b，c，有下列命题：①在△ABC中，A＞B是sinA＞sinB的充分不必要条件；②在△ABC中，A＞B是cosA＜cosB的充要条件；③在△ABC中，A＞B是tanA＞tanB的必要不充分条件．其中正确命题的序号为________．

已知E，F，G，H是空间四点，命题甲：E，F，G，H四点不共面，命题乙：直线EF和GH不相交，则甲是乙成立的________条件．

设函数f(x)＝ax＋b(0≤x≤1)，则a＋2b＞0是f(x)＞0在[0,1]上恒成立的________条件．(填充分但不必要，必要但不充分，充要，既不充分也不必要)

已知“x－a<1”是 “x²－6x<0”的必要不充分条件，则实数a的取值范围________

sinα≠sinβ是α≠β的　　　　　　　条件.

已知不等式x²－2x＋1－a²＜0成立的一个充分条件是0＜x＜4，则实数a的取值范围应满足________．

“a≥0”是“∃x∈R，ax²＋x＋1≥0为真命题”的________条件．

已知集合A＝{x|x＞5}，集合B＝{x|x＞a}，若命题“x∈A”是命题“x∈B”的充分不必要条件，则实数a的取值范围是________．