为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为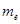 ,众数为
,众数为 ,平均值为
,平均值为 ,则( )
,则( )
A. 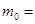  |
B. 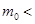  |
C. 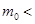  |
D.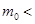   |
若随机变量 服从两点分布,其中
服从两点分布,其中 ,则
,则 和
和 的值分别是( )
的值分别是( )
| A.4和4 | B.4和2 | C.2和4 | D.2和2 |
已知x,y的取值如右表:从散点图可以看出y与x线性相关,且回归方程为,则( )
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
A.3.25 B.2.6 C.2.2 D.0
某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
| 气温x(℃) |
18 |
13 |
10 |
-1 |
| 用电量y(度) |
24 |
34 |
38 |
64 |
由表中数据得线性回归方程 =
=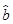 x+
x+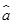 中
中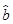 ≈-2,预测当气温为-4℃时,用电量的度数约为( )
≈-2,预测当气温为-4℃时,用电量的度数约为( )
A.58 B.66 C.68 D.70
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间 与数学成绩
与数学成绩 进行数据收集如下:
进行数据收集如下:
| x |
15 |
16 |
18 |
19 |
22 |
| y |
102 |
98 |
115 |
115 |
120 |
由表中样本数据求得回归方程为 ,则点
,则点 与直线
与直线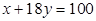 的位置关系是( )
的位置关系是( )
A.点在直线左侧 B.点在直线右侧 C.点在直线上 D.无法确定
设某大学的女生体重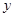 (单位:
(单位: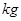 )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据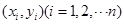 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为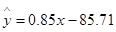 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是( )
| 表1 |
不及格 |
及格 |
总计 |
| 男 |
6 |
14 |
20 |
| 女 |
10 |
22 |
32 |
| 总计 |
16 |
36 |
52 |
A.成绩
| 表2 |
不及格 |
及格 |
总计 |
| 男 |
4 |
16 |
20 |
| 女 |
12 |
20 |
32 |
| 总计 |
16 |
36 |
52 |
B.视力
| 表3 |
不及格 |
及格 |
总计 |
| 男 |
8 |
12 |
20 |
| 女 |
8 |
24 |
32 |
| 总计 |
16 |
36 |
52 |
C.智商
| 表4 |
不及格 |
及格 |
总计 |
| 男 |
14 |
6 |
20 |
| 女 |
2 |
30 |
32 |
| 总计 |
16 |
36 |
52 |
D.阅读量
如图是根据变量x,y的观测数据(xi,yi)(i=1,2,…10)得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是( )
| A.①② | B.①④ | C.②③ | D.③④ |
对于相关系数r下列描述正确的是( )
| A.r>0表明两个变量线性相关性很强 |
| B.r<0表明两个变量无关 |
| C.|r|越接近1,表明两个变量线性相关性越强 |
| D.r越小,表明两个变量线性相关性越弱 |
某公司2005~2010年的年利润x(单位:百万元)与年广告支出y(单位:百万元)的统计资料如表所示:
| 年份 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
| 利润x |
12.2 |
14.6 |
16 |
18 |
20.4 |
22.3 |
| 支出y |
0.62 |
0.74 |
0.81 |
0.89 |
1 |
1.11 |
根据统计资料,则( )
A.利润中位数是16,x与y有正线性相关关系
B.利润中位数是18,x与y有负线性相关关系
C.利润中位数是17,x与y有正线性相关关系
D.利润中位数是17,x与y有负线性相关关系
观察下面频率等高条形图,其中两个分类变量 之间关系最强的是( )
之间关系最强的是( )
A. B. C. D.
观察下面频率等高条形图,其中两个分类变量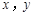 之间关系最强的是( )
之间关系最强的是( )
A. B. C. D.
在育民中学举行的电脑知识竞赛中,将高一两个班参赛学生的成绩(得分的整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图),已知图中从左到右的第一、第二、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05第二小组的频数为40.
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数.
试题篮
()