已知一个线性回归方程为 =2x+45,其中x的取值依次为1, 7, 5, 13, 19,
=2x+45,其中x的取值依次为1, 7, 5, 13, 19,
则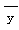 = ( )
= ( )
| A.58.5 | B.46.5 | C.63 | D.75 |
某单位为了制定节能减排的目标,先调查了用电量 (度)与气温
(度)与气温 (℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
由表中数据,得线性回归方程 ,则
,则 = .
= .
废品率x%和每吨生铁成本y(元)之间的回归直线方程为y=256+3x,表明( )
| A.废品率每增加1%,生铁成本增加259元. | B.废品率每增加1%,生铁成本增加3元. |
| C.废品率每增加1%,生铁成本每吨增加3元. | D.废品率不变,生铁成本为256元. |
为了评价某个电视栏目的改革效果,在改革前后分别从某居民点抽取了1000位居民进行调查,经过计算得K2 4.358,根据这一数据分析,下列说法正确的是( )
4.358,根据这一数据分析,下列说法正确的是( )
| A.有95%的人认为该栏日优秀 |
| B.有95%的人认为该栏目是否优秀与改革有关系 |
| C.有95%的把握认为电视栏目是否优秀与改革有关系 |
| D.没有理由认为电视栏目是否优秀与改革有关系 |
已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( )
A. =1.23x+4 B.
=1.23x+4 B. =1.23x+5
=1.23x+5
C =1.23x+0.08 D.
=1.23x+0.08 D. =0.08x+1.23
=0.08x+1.23
下列说法:
①从匀速传递的产品生产流水线上,质检员第10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样
②某地气象局预报:5月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好
④在回归直线方程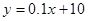 中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位
中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位
其中正确的是 (填上你认为正确的序号)
2012年元旦、春节前夕,各个物流公司都出现了爆仓现象,直接原因就是网上疯狂的购物.某商家针对人们在网上购物的态度在某城市进行了一次调查,共调查了124人,其中女性70人,男性54人.女性中有43人对网上购物持赞成态度,另外27人持反对态度;男性中有21人赞成网上购物,另外33人持反对态度.
(Ⅰ) 估计该地区对网上购物持赞成态度的比例;
(Ⅱ) 有多大的把握认为该地区对网上购物持赞成态度与性别有关;
附:表1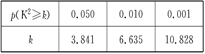
K2=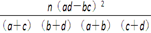
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是( ).
=0.85x-85.71,则下列结论中不正确的是( ).
| A.y与x具有正的线性相关关系 |
B.回归直线过样本点的中心( , , ) ) |
| C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg |
| D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg |
某商场在销售过程中投入的销售成本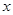 与销售额
与销售额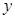 的统计数据如下表:
的统计数据如下表:
| 销售成本x(万元) |
3 |
4 |
6 |
7 |
销售额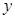 (万元) (万元) |
25 |
34 |
49 |
56 |
根据上表可得,该数据符合线性回归方程: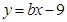 .由此预测销售额为100万元时,投入的销售成本大约为 ;
.由此预测销售额为100万元时,投入的销售成本大约为 ;
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表
| |
患病 |
未患病 |
总计 |
| 没服用药 |
20 |
30 |
50 |
| 服用药 |
x |
y |
50 |
| 总计 |
M |
N |
100 |
设从没服用药的动物中任取两只,未患病数为X;从服用药物的动物中任取两只,未患病数为Y,工作人员曾计算过P(X=0)=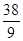 P(Y=0).
P(Y=0).
(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回,抽取5次, 若每次抽取的结果是相互独立的,记被抽取的5头中为服了药还患病的数量为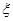 .,求
.,求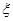 的期望E(
的期望E(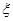 )和方差D(
)和方差D(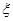 ).
).
参考公式: (其中
(其中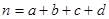 )
)
| P(K2≥k) |
0.25 |
0.15 |
0.10 |
0.05 |
0.010 |
0.005 |
| k |
1.323 |
2.072 |
2.706 |
3.845 |
6.635 |
7.879 |
某市政府调查市民收入增减与旅游愿望的关系时,采用独立性检验法抽查了3 000人,计算发现K2=6.023,则根据这一数据查阅下表,市政府断言市民收入增减与旅游愿望有关系的可信程度是_______。
| P(K2≥k) |
0.25 |
0.15 |
0.10 |
0.025 |
0.010 |
0.005 |
| k |
1.323 |
2.072 |
2.706 |
5.024 |
6.635 |
7.879 |
试题篮
()