一名小学生的年龄和身高(单位:cm)的数据如下:
年龄 |
6 |
7 |
8 |
9 |
身高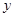 |
118 |
126 |
136 |
144 |
由散点图可知,身高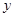 与年龄
与年龄 之间的线性回归直线方程为
之间的线性回归直线方程为 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A.154 B. 153 C.152 D. 151
某种产品的广告费支出 与销售额y之间的(单位:百万元)之间的有如下对应数据:
与销售额y之间的(单位:百万元)之间的有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
y与x之间的线性回归方程为 ,则
,则 =
=
已知x与y之间的一组数据:
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程为y=bx+a必过点__________________________.
有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;
②平均日学习时间和平均学习成绩; ③某人每日吸烟量和其身体健康情况;
④正方形的边长和面积; ⑤汽车的重量和百公里耗油量;
其中两个变量成正相关的是 ( )
| A.①③ | B.②④ | C.②⑤ | D.④⑤ |
若变量 与
与 之间的相关系数
之间的相关系数 ,则变量
,则变量 与
与 之间 ( )
之间 ( )
| A.不具有线性相关关系 |
| B.具有线性相关关系 |
| C.它们的线性相关关系还需要进一步确定 |
| D.不确定 |
.某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x( ) ) |
17 |
13 |
8 |
2 |
| 月销售量y(件) |
24 |
33 |
40 |
55 |
由表中数据算出线性回归方程 中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为_ 件.
中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为_ 件.
(参考公式: )
)
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
| 温差x(℃) |
10 |
11 |
13 |
12 |
8 |
| 发芽y(颗) |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,剩下的2组数据用于回归方程检验.
回归直线方程参考公式:
 ,
, 

(1)请根据12月2日至12月4日的数据,求出y关于x的线性回归方程 ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则
认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(3)请预测温差为14℃的发芽数。
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A.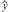 =-10x+200 =-10x+200 |
B.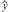 =10x+200 =10x+200 |
C.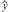 =-10x-200 =-10x-200 |
D.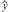 =10x-200 =10x-200 |
下列判断中不正确的是( )
A. 为变量间的相关系数, 为变量间的相关系数, 值越大,线性相关程度越高 值越大,线性相关程度越高 |
| B.在平面直角坐标系中,可以用散点图发现变量之间的变化规律 |
C.线性回归方程代表了观测值 、 、 之间的关系 之间的关系 |
| D.任何一组观测值都能得到具有代表意义的回归直线方程 |
下列函数中,随x(x>0)的增大,增长速度最快的是( )
| A.y =1,x∈Z | B.y=x | C.y=  |
D.y=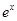 |
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为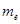 ,众数为
,众数为 ,平均值为
,平均值为 ,则( )
,则( )
A. 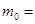  |
B. 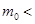  |
C. 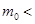  |
D.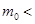   |
废品率 和每吨生铁成本
和每吨生铁成本 (元)之间的回归直线方程为
(元)之间的回归直线方程为 ,这表明 ( )
,这表明 ( )
A. 与 与 的相关系数为2 的相关系数为2 |
B. 与 与 的关系是函数关系的充要条件是相关系数为1 的关系是函数关系的充要条件是相关系数为1 |
| C.废品率每增加1%,生铁成本增加258元 |
| D.废品率每增加1%,生铁成本平均每吨增加2元 |
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
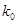 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
试题篮
()