高中数学变量间的相关关系试题

已知、的取值如下表：

从散点图可以看出与线性相关，且回归方程,则.

某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：

该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验。
（1）求选取的2组数据恰好是相邻两个月的概率；
（2）若选取的是1月与6月的两组数据，请根据2至5月份的数据，求出y关于x的线
性回归方程；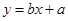
（3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？

已知x，y取值如下表：

x	0	1	4	5	6	8
y	1.3	1.8	5.6	6.1	7.4	9.3

从所得的散点图分析可知：y与x线性相关，且 ＝0.95x＋a，则a＝(   )．
A．1.30      B．1.45      C．1.65          D．1.80

某单位为了了解用电量(千瓦时)与气温()之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：

气温()	18	13	10
用电量(千瓦时)	24	34	38	64

由表中数据得线性回归方程中，预测当气温为时，用电量约为(    )
A．58千瓦时  B．66千瓦时   C．68千瓦时  D．70千瓦时

在线性回归模型中，下列说法正确的是(    )

A．是一次函数

B．因变量是由自变量唯一确定的

C．因变量除了受自变量的影响外，可能还受到其它因素的影响，这些因素会导致随机误差的产生

D．随机误差是由于计算不准确造成的，可以通过精确计算避免随机误差的产生

有下列关系：
①人的年龄与他（她）拥有的财富之间的关系；
②曲线上的点与该点的坐标之间的关系；
③苹果的产量与气候之间的关系；
④森林中的同一种树木，其横断面直径与高度之间的关系，
其中有相关关系的是(    )

A．①②③

B．①②

C．②③

D．①③④

已知变量x，y之间具有线性相关关系，其回归方程为＝－3＋bx，若则b的值为(     )

A．2

B．1

C．－2

D．－1

在研究打酣与患心脏病之间的关系中，通过收集数据、整理分析数据得“打酣与患心脏病有关”的结论，并且有以上的把握认为这个结论是成立的。下列说法中正确的是（   ）

A．100个心脏病患者中至少有99人打酣

B．1个人患心脏病，那么这个人有99%的概率打酣

C．在100个心脏病患者中一定有打酣的人

D．在100个心脏病患者中可能一个打酣的人都没有

为了考察两个变量和之间的线性相关性，甲、乙两位同学各自独立地做100次和150次试验，并且利用线性回归方法，求得回归直线分别为和，已知两人在试验中发现对变量的观测数据的平均值都是，对变量的观测数据的平均值都是，那么下列说法正确的是（     ）

A．和有交点	B．与相交，但交点不一定是
C．与必定平行	D．与必定重合

某种商品的广告费支出与销售额（单位：万元）之间有如下对应数据，根据表中提供的全部数据，用最小二乘法得出与的线性回归方程为，则表中的的值为（     ）

A．45

B．50

C．55

D．60

实验测得四组(x,y)的值分别为(1,2),(2,3),(3,4),(4,4)，则y与x间的线性回归方程是（ ）

A．y＝－1＋x

B．y＝1＋x

C．y＝1.5＋0.7x

D．y＝1＋2x

某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:

零件的个数x(个)	2	3	4	5
加工的时间y(小时)	2.5	3	4	4.5

由表中数据算出线性回归方程=bx+a中的b≈0.7,试预测加工10个零件需_______小时(已知a=-b).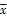

在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):

	物理 成绩好	物理 成绩不好	合计
数学成绩好	62	23	85
数学成绩不好	28	22	50
合计	90	45	135

那么有把握认为数学成绩与物理成绩之间有关的百分比为(　　)
(A)25%　　(B)75%　　(C)95%　　(D)99%

关于线性回归,以下说法错误的是(　　)

A．自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系

B．在平面直角坐标系中用描点的方法得到的表示具有相关关系的两个变量的一组数据的图形叫做散点图

C．线性回归直线方程最能代表观测值x,y之间的关系,且其回归直线一定过样本中心点(,)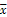

D．甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性作试验,并由回归分析法分别求得相关系数rxy如下表

	甲	乙	丙	丁
rxy	0.82	0.78	0.69	0.85

则甲同学的试验结果体现A,B两变量更强的线性相关性

已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为(　　)

A．=1.23x+4

B．=1.23x+5

C．=1.23x+0.08

D．=0.08x+1.23