某单位为了了解用电量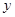 (度)与当天平均气温
(度)与当天平均气温 (°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程
(°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程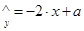 ,则
,则 __________.
__________.
平均气温 (°C) (°C) |
18 |
13 |
10 |
-1 |
用电量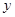 (度) (度) |
25 |
35 |
37 |
63 |
某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,用最小二乘法求出y与x的回归方程 ;
;
(3)预测销售额为115万元时,大约需要多少万元广告费。
参考公式:回归方程为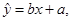 其中
其中 ,
, 
下列关于回归分析的说法正确的是 (填上所有正确说法的序号)
①相关系数 越小,两个变量的相关程度越弱;②残差平方和越大的模型,拟合效果越好;③用相关指数
越小,两个变量的相关程度越弱;②残差平方和越大的模型,拟合效果越好;③用相关指数 来刻画回归效果时,
来刻画回归效果时, 越小,说明模型的拟合效果越好;④用最小二乘法求回归直线方程,是寻求使
越小,说明模型的拟合效果越好;④用最小二乘法求回归直线方程,是寻求使 取最小值时的
取最小值时的 的值;⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
的值;⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
经过长期的观测得到:在交通繁忙的时段内,蚌埠市解放路某路段汽车的车流量 (千辆/h)与汽车的平均速度
(千辆/h)与汽车的平均速度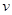 (
(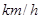 )之间的函数关系为
)之间的函数关系为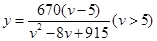 。
。
(1)在该时段内,当汽车的平均速度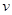 为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
(2)若要求在该时段内车流量超过10千辆/h,则汽车的平均速度应在什么范围内?
人们在生活和消费过程中的过量碳排放,是造成全球气候变暖的重要因素之一,所谓“低碳生活”就是指生活作息时所耗用的能量要尽力减少,从而减低二氧化碳的排放量.某单位为了制定节能减排的目标,先调查了用电量 (度)与气温
(度)与气温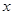 (
(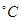 )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温(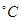 ) ) |
18 |
13 |
10 |
 |
| 用电量(度) |
24 |
34 |
38 |
64 |
由表中数据,得线性回归方程 ,当气温为
,当气温为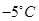 时,预测用电量的度数约为 .
时,预测用电量的度数约为 .
对于下列表格所示的五个散点,已知求得的线性回归直线方程为 =0.8x-155.
=0.8x-155.
| x |
196 |
197 |
200 |
203 |
204 |
| y |
1 |
3 |
6 |
7 |
m |
则实数m的值为( )
A.8.4 B.8.2 C.8 D.8.5
(本小题满分10分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出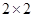 列联表,并判断是否有
列联表,并判断是否有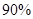 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
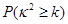 |
0.100 |
0.050 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
6.635 |
10.828 |
 .
.
已知x,y取值如表:
| x |
0 |
1 |
4 |
5 |
6 |
7 |
8 |
9 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.0 |
9.3 |
9.1 |
从所得的散点图分析可知,y与x线性相关,且y=0.95x+a,则a=( )
A.1.30 B.1.45 C.1.65 D.1.80
.已知某种产品的支出广告额 与利润额
与利润额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
| x |
3 |
4 |
5 |
6 |
7 |
| y |
20 |
30 |
30 |
40 |
60 |
则回归直线方程必过( )
A.(5,30) B.(4,30) C.(5,35) D.(5,36)
一名小学生的年龄和身高(单位:cm)的数据如下表:

由散点图可知,身高 与年龄
与年龄 之间的线性回归方程为
之间的线性回归方程为 ,则
,则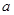 的值为( )
的值为( )
| A.65 | B.74 | C.56 | D.47 |
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程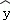 =
=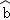 x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
58 |
A.112.1万元 B.113.1万元 C.111.9万元 D.113.9万元
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
单价 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量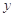 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
由表中数据,求得线性回归方程为 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
试题篮
()