高中数学变量间的相关关系试题

工人月工资y（元）与劳动生产率x（千元）变化的回归方程，下列判断正确的是  (     )　
①劳动生产率为1千元时，工资约为130元　
②劳动生产率提高1千元时，月工资约提高80元　
③劳动生产率提高1千元时，月工资约提高130元　
④当月工资为210元时，劳动生产率约为2千元　

A．① ②

B．① ② ④

C．② ④

D．① ② ③ ④

已知、之间的一组数据如右表：

	0	1	2	3
	8	2	6	4

则线性回归方程所表示的直线必经过点 (       )
A．（0，0）         B．（1.5,5）         C．（4,1.5）          D．（2,2）

设某大学的女生体重（单位：kg）与身高（单位：cm） 具有线性相关关系，根据一组样本数据（，）（i=1，2，…，n），用最小二乘法建立的回归方程为
=0.85x-85.71，则下列结论中不正确的是 (    )

A．与具有正的线性相关关系

B．回归直线过样本点的中心（，）

C．若该大学某女生身高为170cm，则可断定其体重必为58.79kg

D．若该大学某女生身高增加1cm，则其体重约增加0.85kg

下列关于由最小二乘法求出的回归直线方程 =2－x的说法中，不正确的是

A．变量x与y正相关

B．该回归直线必过样本点中心（）

C．当x=l时，y的预报值为l

D．当残差平方和越小时模型拟合的效果越好

某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是(　　)

A．＝－10x＋200	B．＝10x＋200
C．＝－10x－200	D．＝10x－200

在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520个女性中6人患色盲，
（1）根据以上的数据建立一个2×2的列联表；
（2）若认为“性别与患色盲有关系”，则出错的概率会是多少
（本题可以参考两个分类变量x和y有关系的可信度表:）

为研究变量和的线性相关性，甲、乙二人分别作了研究，利用线性回归方法得到回归直线方程和，两人计算知相同，也相同，下列正确的是：

A．与重合	B．与一定平行
C．与相交于点	D．无法判断和是否相交

在回归直线方程   （   ）

A．当，的平均值

B．当变动一个单位时，的实际变动量

C．当变动一个单位时，的平均变动量

D．当变动一个单位时，的平均变动量

根据一组样本数据的散点图分析存在线性相关关系，求得其回归方程，则在样本点处的残差为（   ）

A．

B．

C．

D．

对具有线性相关关系的的变量，，测得一组数据如下表

	2	4	5	6	8
	20	40	60	70	80

根据上表，利用最小二乘法得它们的回归直线方程为，据此模型来预测当时，的估计值为 （   ）
A.210   B.210.5 C.211.5 D.212.5

某商品销售量y（件）与销售价格x（元/件）负相关，则其回归方程可能是(    )

A．	B．
C．	D．

某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：

单价x（元）	8	8.2	8.4	8.6	8.8	9
销量y (件 )	90	84	83	80	75	68

（I）求销量与单价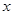间的回归直线方程；
（II）预计在今后的销售中，销量与单价仍然服从（I）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？

在一段时间内，某种商品价格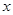（万元）和需求量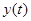之间的一组数据为：

价 格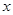	1.4	1.6	1.8	2	2.2
需求量	12	10	7	5	3

（1）进行相关性检验；
（2）如果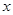与之间具有线性相关关系，求出回归直线方程，并预测当价格定为1.9万元，需求量大约是多少？（精确到0.01）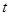
参考公式及数据：，，
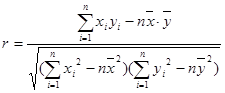相关性检验的临界值表：

n-2	1	2	3	4	5	6	7	8	9	10
小概率0.01	1.000	0.990	0.959	0.917	0.874	0.834	0.798	0.765	0.735	0.708

利用独立性检验来考虑两个分类变量X和Y是否有关系时，通过查阅下表来确定断言“X和Y有关系”的可信度。如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为(     )

P(k^2>k)	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	2.072	2.706	3.84	5.024	6.635	7.879	10.83

A.25％         B.75％            C.2.5％          D.97.5％

如果数据、、…… 的平均值为，方差为 ，则，，…… 的平均值和方差分别为（      ）

A．和	B．3+5和9
C．3+5和	D．3+5 和9+30+25