某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是( )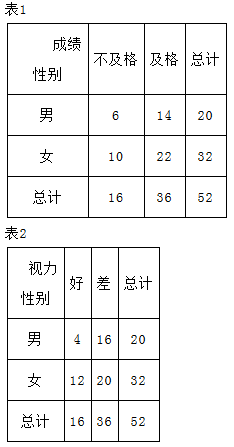
| A.成绩 | B.视力 | C.智商 | D.阅读量 |
经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度 (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为: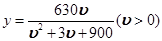 .问:在该时段内,当汽车的平均速度
.问:在该时段内,当汽车的平均速度 等于 时,车流量最大?
等于 时,车流量最大?
对于函数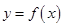 ,部分
,部分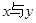 的对应关系如下表:
的对应关系如下表:
数列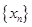 满足:
满足: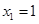 ,且对于任意
,且对于任意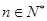 ,点
,点 都在函数
都在函数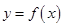 的图象上,则
的图象上,则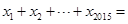 ( )
( )
| A.7539 | B.7546 | C.7549 | D.7554 |
根据如下样本数据得到的回归方程为 =bx+a,则( )
=bx+a,则( )
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4.0 |
2.5 |
-0.5 |
0.5 |
-2.0 |
-3.0 |
A.a>0,b<0 B.a>0,b>0 C.a<0,b<0 D.a<0,b>0
已知变量和
满足关系
,变量
与
正相关. 下列结论中正确的是()
| A. |
|
| B. |
|
| C. |
|
| D. |
|
为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
| 收入
(万元) |
8.2 |
8.6 |
10.0 |
11.3 |
11.9 |
| 支出
(万元) |
6.2 |
7.5 |
8.0 |
8.5 |
9.8 |
根据上表可得回归直线方程
,其中
,据此估计,该社区一户收入为15万元家庭年支出为( )
| A. |
11.4万元 |
B. |
11.8万元 |
C. |
12.0万元 |
D. |
12.2万元 |
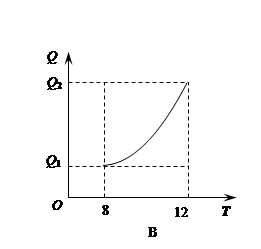
水厂监控某一地区居民用水情况,该地区A,B,C,D四个小区在8:00—12:00时用水总量Q与时间t的函数关系如图所示,在这四个小区中,单位时间内用水量逐步增加的是( )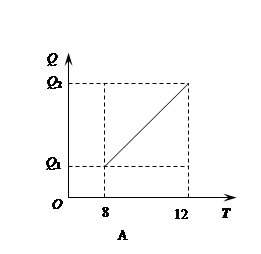


根据如下样本数据
| x |
3 |
4 |
5 |
6 |
7 |
| y |
4.0 |
2.5 |
 0.5 0.5 |
0.5 |
 2.0 2.0 |
得到的回归方程为 .若
.若 ,则
,则 每增加1个单位,
每增加1个单位, 就( ).
就( ).
A.增加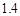 个单位 B.减少
个单位 B.减少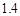 个单位
个单位
C.增加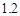 个单位 D.减少
个单位 D.减少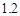 个单位
个单位
某单位为了了解用电量y度与气温x0C之间的关系随机统计了某4天的用电量与当天气温
| 气温(0C) |
14 |
12 |
8 |
6 |
| 用电量 |
22 |
26 |
34 |
38 |
(1)求用电量y与气温x的线性回归方程;
(2)由(1)的方程预测气温为50C时,用电量的度数。
参考公式:
(本小题满分12分)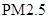 是指空气中直径小于或等于
是指空气中直径小于或等于 微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
微米的颗粒物(也称可入肺颗粒物).为了探究车流量与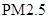 的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与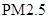 的数据如下表:
的数据如下表:
| 时间 |
周一 |
周二 |
周三 |
周四 |
周五 |
车流量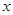 (万辆) (万辆) |
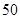 |
 |
 |
 |
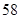 |
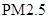 的浓度 的浓度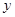 (微克/立方米) (微克/立方米) |
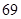 |
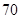 |
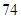 |
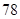 |
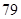 |
(1)根据上表数据,请在下列坐标系中画出散点图;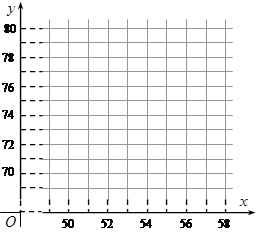
(2)根据上表数据,用最小二乘法求出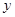 关于
关于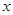 的线性回归方程
的线性回归方程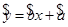 ;
;
(3)若周六同一时间段车流量是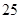 万辆,试根据(2)求出的线性回归方程预测,此时
万辆,试根据(2)求出的线性回归方程预测,此时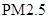 的浓度为多少(保留整数)?
的浓度为多少(保留整数)?
一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度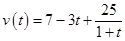 (
( 的单位:
的单位: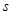 ,
, 的单位:
的单位: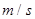 )行驶至停止.在此期间汽车继续行驶的距离(单位:
)行驶至停止.在此期间汽车继续行驶的距离(单位: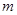 )是( ).
)是( ).
A.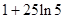 |
B. |
C.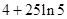 |
D. |
2015年,各大品牌汽车继续在中国的汽车市场上相互博弈,汽车的配置与销售价格以及维修费用等成为人们购买汽车时需要考虑的因素,某汽车制造商为了进一步拓宽市场,统计了某种品牌的汽车的使用年限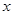 和所支出的维修费用
和所支出的维修费用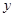 (万元),得到的统计资料:
(万元),得到的统计资料:
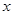 |
2 |
3 |
4 |
5 |
6 |
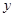 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料可知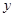 对
对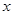 呈线性相关关系,且线性回归方程为
呈线性相关关系,且线性回归方程为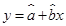 ,其中已知
,其中已知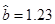 ,根据国家政策规定,轿车取消报废年限,若该品牌汽车在使用10年时报废,则这10年的维修总费用约为_________.
,根据国家政策规定,轿车取消报废年限,若该品牌汽车在使用10年时报废,则这10年的维修总费用约为_________.
(本小题满分10分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出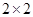 列联表,并判断是否有
列联表,并判断是否有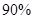 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
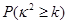 |
0.100 |
0.050 |
0.010 |
0.001 |
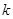 |
2.706 |
3.841 |
6.635 |
10.828 |
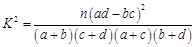 .
.
通过随机询问110名大学生是否爱好某项运动,得到如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由上表算得k≈7.8,因此得到的正确结论是( )
| P(k2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
试题篮
()