某商店统计了最近6个月某商品的进价x(元)与售价y(元)的对应数据如下表:
| x |
3 |
5 |
2 |
7 |
8 |
11 |
| y |
4 |
6 |
3 |
9 |
12 |
14 |
则回归直线方程是_______________.
注:线性回归直线方程系数公式: 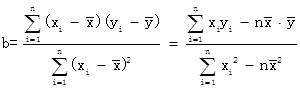 ,a=y-bx
,a=y-bx
一机器可以按各种不同的速度运转,其生产物件有一些会有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用 表示转速(单位转/秒),用
表示转速(单位转/秒),用 表示每小时生产的有缺点物件个数,现观测得到
表示每小时生产的有缺点物件个数,现观测得到 的4组观测值为(8,5),(12,8),(14,9),(16,11).
的4组观测值为(8,5),(12,8),(14,9),(16,11).
(1)假定 与
与 之间有线性相关关系,求
之间有线性相关关系,求 对
对 的回归直线方程.
的回归直线方程.
(2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒?(精确到1转/秒)
(参考公式 )
)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为 .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
在2014年元旦期间,某市物价部门对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如表所示:
| 价格x |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y |
11 |
10 |
8 |
6 |
5 |
通过分析,发现销售量y与商品的价格x具有线性相关关系,则销售量y关于商品的价格x的线性回归方程为__________.
进入4月份,天气渐暖,蔬菜上市品种逐渐增加.某蔬菜销售市场,根据连续5周的市场调研,对某种蔬菜的销售量 (千克)与价格
(千克)与价格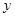 (元∕千克)统计数据(如表所示)表明:二者负相关,其回归方程为
(元∕千克)统计数据(如表所示)表明:二者负相关,其回归方程为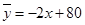 ,则统计表格中的实数
,则统计表格中的实数 的值为( )
的值为( )
| 周次 |
1 |
2 |
3 |
4 |
5 |
销售量 |
18 |
19 |
18 |
22 |
23 |
价格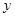 |
45 |
43 |
 |
35 |
33 |
A.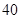 B.
B.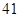 C.
C.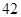 D.
D.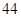
给出下列五个命题:
①某班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知7号,33号,46号同学在样本中,那么样本另一位同学的编号为23;
②一组数据1、2、3、3、4、5的平均数、众数、中位数相同;
③一组数据a、0、1、2、3,若该组数据的平均值为1,则样本标准差为2;
④根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为
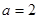 ,
,  ,则
,则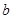 =1;
=1;
⑤如图是根据抽样检测后得出的产品样本净重(单位:克)数据绘制的频率分布直方图,已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克,并且小于104克的产品的个数是90.
其中真命题为: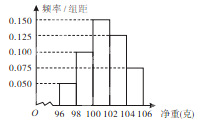
| A.①②④ | B.②④⑤ | C.②③④ | D.③④⑤ |
某种产品的广告费支出x与销售额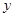 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
50 |
60 |
70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 .
.
(3)经计算,相关指数 ,你可得到什么结论?
,你可得到什么结论?
(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
下表提供了某厂节能降耗技术改造后在生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗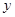 (吨)的几组对应数据:
(吨)的几组对应数据:
 |
3 |
4 |
5 |
6 |
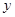 |
2.5 |
3 |
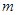 |
4.5 |
若根据上表提供的数据用最小二乘法可求得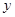 对
对 的回归直线方程是
的回归直线方程是 0.7
0.7 +0.35,则表中
+0.35,则表中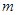 的值为( )
的值为( )
A.4 B.4.5 C.3 D.3.5
观察下列关于两个变量 和
和 的三个散点图,它们从左到右的对应关系依次为( )
的三个散点图,它们从左到右的对应关系依次为( )
| A.正相关、负相关、不相关 | B.负相关、不相关、正相关 |
| C.负相关、正相关、不相关 | D.正相关、不相关、负相关 |
设是变量
和
的
个样本点,直线
是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )
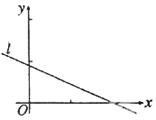
| A. |
|
| B. |
|
| C. |
当
|
| D. |
直线
|
下表是某旅游区游客数量与平均气温的对比表:
| 平均气温(℃) |
-1 |
4 |
10 |
13 |
18 |
26 |
| 数量(百个) |
20 |
24 |
34 |
38 |
50 |
64 |
若已知游客数量与平均气温是线性相关的,则回归方程为( ).
A. =1.98x+22.13
=1.98x+22.13
B. =1.78x+20.13
=1.78x+20.13
C. =1.68x+18.73
=1.68x+18.73
D. =1.51x+15.73
=1.51x+15.73
一般来说,一个人脚越长,他的身高就越高.现对10名成年人的脚长x(单位:cm)与身高y(单位:cm)进行测量,得如下数据:
| x |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
| y |
141 |
146 |
154 |
160 |
169 |
176 |
181 |
188 |
197 |
203 |
作出散点图后,发现散点在一条直线附近.
经计算得到一些数据: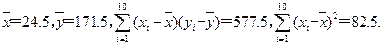
某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长26.5 cm,请你估计案发嫌疑人的身高为( )
A.185 B.185.5 C.186 D.186.5
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)若日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?
(2)从这6名工人中任取2人,设这两人加工零件的个数分别为 ,求
,求 的概率.
的概率.
某学生课外活动兴趣小组对两个相关变量收集到5组数据如下表:
| x |
10 |
20 |
30 |
40 |
50 |
| y |
62 |
■ |
75 |
81 |
89 |
由最小二乘法求得回归方程为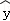 =0.67x+54.9,现发现表中有一个数据模糊不清,请推断该点数据的值为( )
=0.67x+54.9,现发现表中有一个数据模糊不清,请推断该点数据的值为( )
A.67 B.68 C.69 D.70
试题篮
()