高中数学变量间的相关关系选择题

通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的
列联表：

	男	女	总计
爱好	40	20	60
不爱好	20	30	50
总计	60	50	110

由算得，
附表： 

	0.050	0.010	0.001
k	3.841	6.635	10.828

参照附表，得到的正确结论是（  ）
A、有99%以上的把握认为“爱好该项运动与性别有关”
B、有99%以上的把握认为“爱好该项运动与性别无关”
C、在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别有关”
D、在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别无关”

通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列

由算得，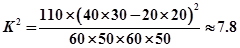
．
参照附表，得到的正确结论是 （  ）

A．再犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别有关”

B．再犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别无关”

C．有99%以上的把握认为“爱好该项运动与性别有关”

D．有99%以上的把握认为“爱好该项运动与性别无关”

如图所示，图中有5组数据，去掉　　　组数据后（填字母代号），剩下的4组数据的线性相关性最强（     ）

A．

B．

C．

D．

我校开展研究性学习活动，高二某同学获得一组实验数据如下表：

x	1.99	3	4	5.1	6.12
y	1.5	4.04	7.5	12	18.01

对于表中数据，现给出以下拟合曲线，其中拟合程度最好的是
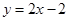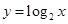A.          B.    C.       D.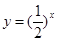

为了评价某个电视栏目的改革效果，在改革前后分别从居民点抽取了100位居民进行调查，经过计算K²≈0.99,根据这一数据分析，下列说法正确的是

A．有99%的人认为该栏目优秀

B．有99%的人认为该栏目是否优秀与改革有关系

C．有99%的把握认为电视栏目是否优秀与改革有关系

D．没有理由认为电视栏目是否优秀与改革有关系

.三点（3，10），（7，20）,(11,24)的回归方程是

A．y=5-17x	B．y=-17+5x
C． y=17+5x	D． y=17-5x

.设有一个回归方程y=3-5x则变量x增加一个单位时

A．y平均减少5个单位	B．y平均增加3个单位.
C．y平均减少3个单位	D．y平均增加5个单位.

.在下列各图中，每个图的两个变量具有相关关系的图是（   ）
       
        （1）             （2）         （3）          （4）

A．（1）（2）

B．（1）（3）

C．（2）（4）

D．（2）（3）

有五组变量：①汽车的重量和汽车每消耗1升汽油所行驶的平均路程；
②平均日学习时间和平均学习成绩；   ③某人每日吸烟量和其身体健康情况；
④正方形的边长和面积；             ⑤汽车的重量和百公里耗油量；
其中两个变量成正相关的是     （   ）

A．①③

B．②④

C．②⑤

D．④⑤

下列关系中，具有相关关系的是（   ）

A．人的身高与体重；	B．匀速行驶的车辆所行驶距离与行驶的时间；
C．人的身高与视力；	D．正方体的体积与边长.

下表是x与y之间的一组数据，则y关于x的线性回归直线必过点(    )

x	0	1	2	3
y	1	3	5	7

 
A.(2,2)       B.(1.5,2)    C.(1,2)       D.(1.5,4)

对四组数据进行统计，获得以下散点图，关于其线性相关系数比较，正确的是（  ）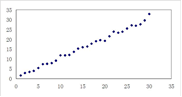
     
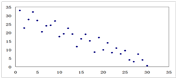
线性相关系数为                 线性相关系数为
     
线性相关系数为                 线性相关系数为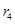

A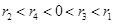．	B．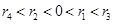
C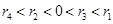．	D．

已知x与y之间的一组数据：

x	0	1	2	3
y	1	3	5	7

则y与x的线性回归方程为y=bx+a必过点         D
A .(2,2)   B.(1,2)    C.(1.5,0)     D (1.5,4)

下列两变量中不存在相关关系的是
①人的身高与视力；②曲线上的点与该点的坐标之间的关系；③某农田的水稻产量与施肥量；④某同学考试成绩与复习时间的投入量；⑤匀速行驶的汽车的行驶的距离与时间；⑥家庭收入水平与纳税水平；⑦商品的销售额与广告费.

A．①②⑤

B．①③⑦

C．④⑦⑤

D．②⑥⑦

在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是

A．若K^2的观测值为k=6.635,而P(K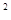≥6.635) =0.010，故我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病

B．若从统计量中求出有95% 的把握认为吸烟与患肺病有关系，是指有5% 的可能性使得推断出现错误

C．从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病

D．以上三种说法都不正确