.三点(3,10),(7,20),(11,24)的回归方程是
| A.y=5-17x | B.y=-17+5x |
| C. y=17+5x | D. y=17-5x |
下列关系中,具有相关关系的是( )
| A.人的身高与体重; | B.匀速行驶的车辆所行驶距离与行驶的时间; |
| C.人的身高与视力; | D.正方体的体积与边长. |
设某大学的女生体重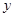 (单位:
(单位: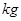 )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据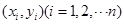 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为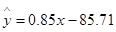 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.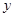 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心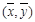 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
对四组数据进行统计,获得以下散点图,关于其线性相关系数比较,正确的是( )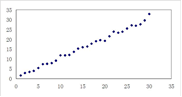

线性相关系数为 线性相关系数为
线性相关系数为

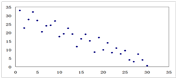
线性相关系数为 线性相关系数为
线性相关系数为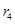
A.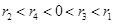 |
B.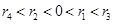 |
C.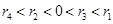 |
D. |
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是( ).
=0.85x-85.71,则下列结论中不正确的是( ).
| A.y与x具有正的线性相关关系 |
B.回归直线过样本点的中心( , , ) ) |
| C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg |
| D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg |
下列两变量中不存在相关关系的是
①人的身高与视力;②曲线上的点与该点的坐标之间的关系;③某农田的水稻产量与施肥量;④某同学考试成绩与复习时间的投入量;⑤匀速行驶的汽车的行驶的距离与时间;⑥家庭收入水平与纳税水平;⑦商品的销售额与广告费.
| A.①②⑤ | B.①③⑦ | C.④⑦⑤ | D.②⑥⑦ |
某科研所共有职工 人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
A.年龄数据的中位数是 ,众数是 ,众数是 |
| B.年龄数据的中位数和众数一定相等 |
C.年龄数据的平均数 |
| D.年龄数据的平均数一定大于中位数 |
下列判断中不正确的是( )
A. 为变量间的相关系数, 为变量间的相关系数, 值越大,线性相关程度越高 值越大,线性相关程度越高 |
| B.在平面直角坐标系中,可以用散点图发现变量之间的变化规律 |
C.线性回归方程代表了观测值 、 、 之间的关系 之间的关系 |
| D.任何一组观测值都能得到具有代表意义的回归直线方程 |
下列函数中,随x(x>0)的增大,增长速度最快的是( )
| A.y =1,x∈Z | B.y=x | C.y=  |
D.y=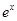 |
对具有线性相关关系的变量x,y有一组观测数据(xi,yi)( i=1,2,…,8),其回归直线方程是 =
=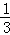 x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
A.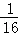 |
B.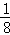 |
C.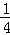 |
D. |
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间 与数学成绩
与数学成绩 进行数据收集如下:
进行数据收集如下:
| x |
15 |
16 |
18 |
19 |
22 |
| y |
102 |
98 |
115 |
115 |
120 |
由表中样本数据求得回归方程为 ,则点
,则点 与直线
与直线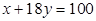 的位置关系是( )
的位置关系是( )
A.点在直线左侧 B.点在直线右侧 C.点在直线上 D.无法确定
为了评价某个电视栏目的改革效果,在改革前后分别从某居民点抽取了1000位居民进行调查,经过计算得K2 4.358,根据这一数据分析,下列说法正确的是( )
4.358,根据这一数据分析,下列说法正确的是( )
| A.有95%的人认为该栏日优秀 |
| B.有95%的人认为该栏目是否优秀与改革有关系 |
| C.有95%的把握认为电视栏目是否优秀与改革有关系 |
| D.没有理由认为电视栏目是否优秀与改革有关系 |
试题篮
()