下列说法错误的是( )
| A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系; |
B.线性回归方程对应的直线 = = x+ x+ 至少经过其样本数据(x1,y1),(x2,y2),,(xn,yn)中的一个点; 至少经过其样本数据(x1,y1),(x2,y2),,(xn,yn)中的一个点; |
| C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高; |
D.在回归分析中, 为0.98的模型比 为0.98的模型比 为0.80的模型拟合的效果好. 为0.80的模型拟合的效果好. |
给出以下四个说法:
①在匀速传递的产品生产流水线上,质检员每间隔 分钟抽取一件产品进行某项指标的检测 ,这样的抽样是分层抽样;
分钟抽取一件产品进行某项指标的检测 ,这样的抽样是分层抽样;
②在刻画回归模型的拟合效果时,相关指数 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程 中,当解释变量
中,当解释变量 每增加一个单位时,预报变量
每增加一个单位时,预报变量 平均增加
平均增加 个单位;
个单位;
④对分类变量 与
与 ,若它们的随机变量
,若它们的随机变量 的观测值
的观测值 越小,则判断“
越小,则判断“ 与
与 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是
| A.①④ | B.②④ | C.①③ | D.②③ |
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲,乙,丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )

| A.消耗1升汽油,乙车最多可行驶5千米 |
| B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 |
| C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油 |
| D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油 |
设有一个线性回归直线方程为 ,则变量
,则变量 每增加一个单位时( )
每增加一个单位时( )
A. 平均增加 1.5 个单位 平均增加 1.5 个单位 |
B. 平均增加 2 个单位 平均增加 2 个单位 |
C. 平均减少 1.5 个单位 平均减少 1.5 个单位 |
D. 平均减少 2 个单位 平均减少 2 个单位 |
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据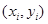 (
( ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为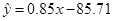 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心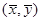 |
C.若该大学某女生身高增加 ,则其体重约增加 ,则其体重约增加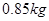 |
D.若该大学某女生身高为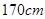 ,则可断定其体重为 ,则可断定其体重为 |
某产品的广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
据上表得回归方程 为9.4,据此预报广告费用为6万元时销售额约为( )
为9.4,据此预报广告费用为6万元时销售额约为( )
A、63.6万元 B、65.5万元 C、67.7万元 D、72.0万元
一名小学生的年龄和身高(单位:cm)的数据如下表:

由散点图可知,身高 与年龄
与年龄 之间的线性回归方程为
之间的线性回归方程为 ,则
,则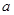 的值为( )
的值为( )
| A.65 | B.74 | C.56 | D.47 |
为了解某商品销售量 (单位:件)与销售价格
(单位:件)与销售价格 (单位:元/件)的关系,统计了(
(单位:元/件)的关系,统计了( )的10组值,并画成散点图如图,则其回归方程可能是
)的10组值,并画成散点图如图,则其回归方程可能是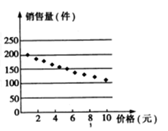
A. |
B.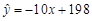 |
C.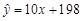 |
D. |
对于下列表格所示的五个散点,已知求得的线性回归直线方程为 =0.8x-155.
=0.8x-155.
| x |
196 |
197 |
200 |
203 |
204 |
| y |
1 |
3 |
6 |
7 |
m |
则实数m的值为( )
A.8.4 B.8.2 C.8 D.8.5
下列反映两个变量的相关关系中,不同于其它三个的是
| A.名师出高徒 | B.水涨船高 | C.月明星稀 | D.登高望远 |
若变量 与
与 之间的相关系数
之间的相关系数 ,则变量
,则变量 与
与 之间
之间
| A.不具有线性相关关系 |
| B.具有线性相关关系 |
| C.它们的线性相关关系还需要进一步确定 |
| D.不确定 |
已知变量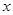 与
与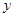 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数 ,
,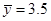 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )
A.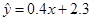 |
B.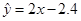 |
C.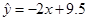 |
D.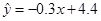 |
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) |
3.0 |
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
| 销量y(瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知的关系符合线性回归方程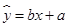 ,其中
,其中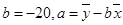 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
试题篮
()