以下正确命题的个数为( )
①命题“存在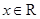 ,
,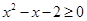 ”的否定是:“不存在
”的否定是:“不存在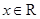 ,
,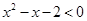 ”;
”;
②函数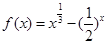 的零点在区间
的零点在区间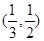 内;
内;
③ 函数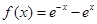 的图象的切线的斜率的最大值是
的图象的切线的斜率的最大值是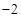 ;
;
④线性回归直线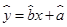 恒过样本中心
恒过样本中心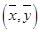 ,且至少过一个样本点.
,且至少过一个样本点.
A. |
B. |
C.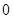 |
D.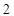 |
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法求得回归直线方程 ,表中有一个数据模糊不清,请你推断出该数据的值为( )
,表中有一个数据模糊不清,请你推断出该数据的值为( )
| A.75 | B.62 | C.68 | D.81 |
某小卖部销售一品牌饮料的零售价 (元/瓶)与销量
(元/瓶)与销量 (瓶)的关系统计如下:
(瓶)的关系统计如下:
零售价 (元/瓶) (元/瓶) |
 |
 |
 |
 |
 |
 |
销量 (瓶) (瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知 的关系符合线性回归方程
的关系符合线性回归方程 ,其中
,其中 ,
, .当单价为
.当单价为 元时,估计该小卖部销售这种品牌饮料的销量为 ( )
元时,估计该小卖部销售这种品牌饮料的销量为 ( )
A.  B.
B. C.
C. D.
D.
某车间加工零件的数量 与加工时间
与加工时间 的统计数据如表:
的统计数据如表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A、84分钟 B、94分钟 C、102分钟 D、112分钟
四名同学根据各自的样本数据研究变量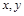 之间的相关关系,并求得回归直线方程,
之间的相关关系,并求得回归直线方程,
分别得到以下四个结论:
① y与x负相关且 ;
;
② y与x负相关且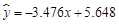 ;
;
③ y与x正相关且 ;
;
④ y与x正相关且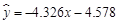 .
.
其中一定不正确的结论的序号是__________.
| A.①② | B.②③ | C.③④ | D.①④ |
已知两个变量x,y之间具有线性相关关系,试验测得(x,y)的四组值分别为(1,2),(2,4),(3,5),(4,7),则y与x之间的回归直线方程为( )
| A.y=0.8x+3 | B.y=-1.2x+7.5 |
| C.y=1.6x+0.5 | D.y=1.3x+1.2 |
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为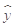 =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )
| A.y与x具有正的线性相关关系 |
B.回归直线过样本点的中心(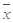 , , ) ) |
| C.若该大学某女生身高增加1cm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重比为58.79kg |
某车间生产一种玩具,为了要确定加工玩具所需要的时间,进行了10次实验,数据如下:
| 玩具个数 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
| 加工时间 |
4 |
7 |
12 |
15 |
21 |
25 |
27 |
31 |
37 |
41 |
如回归方程的斜率是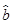 ,则它的截距是 ( )
,则它的截距是 ( )
A.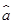 =11
=11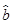 -22; B.
-22; B.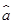 =11-22
=11-22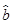 ; C.
; C.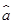 =22-11
=22-11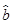 ; D.
; D.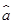 =22
=22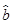 -11.
-11.
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 天 天 |
1 |
2 |
3 |
4 |
5 |
被感染的计算机数量 (台) (台) |
10 |
20 |
39 |
81 |
160 |
则下列函数模型中能较好地反映计算机在第 天被感染的数量
天被感染的数量 与
与 之间的关系的是 ( )
之间的关系的是 ( )
A. B.
B. C.
C. D.
D.
下列命题正确的有
①用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
②命题 :“
:“ ”的否定
”的否定 :“
:“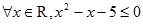 ”;
”;
③设随机变量 服从正态分布
服从正态分布 , 若
, 若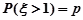 ,则
,则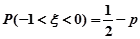 ;
;
④回归直线一定过样本中心(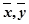 ).
).
| A.1个 | B.2个 | C.3个 | D.4个 |
某学生四次模拟考试时,其英语作文的减分情况如下表:
| 考试次数x |
1 |
2 |
3 |
4 |
| 所减分数y |
4.5 |
4 |
3 |
2.5 |
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为
A.
B.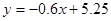
C.
D.
一项研究要确定是否能够根据施肥量预测作物的产量。这里的预报释变量是( )
| A.作物的产量 | B.施肥量 |
| C.试验者 | D.降雨量或其他解释产量的变量 |
试题篮
()