下表是某厂1—4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归方程为 =-0.7x+a,则a等于( )
=-0.7x+a,则a等于( )
A.10.5 B.5.15 C.5.2 D.5.25
下列说法中正确的有( )
①若r>0,则x增大时,y也相应增大; ②若r<0,则x增大时,y也相应增大;
③若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个点均在一条直线上.
| A.①② | B.②③ | C.①③ | D.①②③ |
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间 与数学成绩
与数学成绩 进行数据收集如下:
进行数据收集如下:
| x |
15 |
16 |
18 |
19 |
22 |
| y |
102 |
98 |
115 |
115 |
120 |
由表中样本数据求得回归方程为 ,则点
,则点 与直线
与直线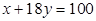 的位置关系是( )
的位置关系是( )
A.点在直线左侧 B.点在直线右侧 C.点在直线上 D.无法确定
在一次独立性检验中,有300人按性别和是否色弱分类如下表:
| |
男 |
女 |
| 正常 |
130 |
120 |
| 色弱 |
20 |
30 |
由此表计算得统计量K2=( ).
(参考公式: )
)
A.2 B.3 C.2.4 D.3.6
设某大学的女生体重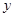 (单位:
(单位: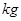 )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据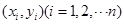 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为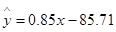 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.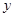 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心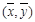 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到数据如表.预计在今后的销售中,销量与单价仍然服从 (
(  ,
, )的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入-成本),该产品的单价应定为( )元
)的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入-成本),该产品的单价应定为( )元
单价 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
A. B.8 C.
B.8 C. D.
D.
两个变量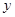 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1的相关指数 为0.98 为0.98 |
B.模型2的相关指数 为0.80 为0.80 |
C.模型3的相关指数 为0.50 为0.50 |
D.模型4的相关指数 为0.25 为0.25 |
对相关系数r,下列说法正确的是
A. 越大,线性相关程度越大 越大,线性相关程度越大 |
B. 越小,线性相关程度越大 越小,线性相关程度越大 |
C. 越大,线性相关程度越小, 越大,线性相关程度越小, 越接近0,线性相关程度越大 越接近0,线性相关程度越大 |
D. 且 且 越接近1,线性相关程度越大, 越接近1,线性相关程度越大, 越接近0,线性相关程度越小 越接近0,线性相关程度越小 |
已知x,y的取值如下表所示,若y与x线性相关,且
| x |
0 |
1 |
3 |
4 |
 |
2.2 |
4.3 |
4.8 |
6.7 |
A.2.2 B.2.6 C.2.8 D.2.9
某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是( )
| 表1 |
不及格 |
及格 |
总计 |
| 男 |
6 |
14 |
20 |
| 女 |
10 |
22 |
32 |
| 总计 |
16 |
36 |
52 |
A.成绩
| 表2 |
不及格 |
及格 |
总计 |
| 男 |
4 |
16 |
20 |
| 女 |
12 |
20 |
32 |
| 总计 |
16 |
36 |
52 |
B.视力
| 表3 |
不及格 |
及格 |
总计 |
| 男 |
8 |
12 |
20 |
| 女 |
8 |
24 |
32 |
| 总计 |
16 |
36 |
52 |
C.智商
| 表4 |
不及格 |
及格 |
总计 |
| 男 |
14 |
6 |
20 |
| 女 |
2 |
30 |
32 |
| 总计 |
16 |
36 |
52 |
D.阅读量
根据如下样本数据:
| 3 |
4 |
5 |
6 |
7 |
8 |
|
| 4.0 |
2.5 |
-0.5 | 0.5 |
-2.0 | -3.0 |
得到的回归方程为,则( )
A. ,
B.
,
C. ,
D.
,
已知变量 与 正相关,且由观测数据算得样本平均数 ,则由该观测的数据算得的线性回归方程可能是
| A. | B. | ||
| C. | D. |
根据如下样本数据
| 3 |
4 |
5 |
6 |
7 |
8 |
|
| 4.0 |
2.5 |
-0.5 | 0.5 |
-2.0 | -3.0 |
得到的回归方程为,则()
| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()