下列结论:①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.其中正确的是 .(将所有正确的序号填上)
下列说法:
①从匀速传递的产品生产流水线上,质检员第10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样
②某地气象局预报:5月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好
④在回归直线方程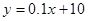 中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位
中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位
其中正确的是 (填上你认为正确的序号)
随机变量X的分布列为
| X |
1 |
2 |
4 |
| P |
0.5 |
0.2 |
0.3 |
则E(3X+4)=________.
某市政府调查市民收入增减与旅游愿望的关系时,采用独立性检验法抽查了3 000人,计算发现K2=6.023,则根据这一数据查阅下表,市政府断言市民收入增减与旅游愿望有关系的可信程度是_______。
| P(K2≥k) |
0.25 |
0.15 |
0.10 |
0.025 |
0.010 |
0.005 |
| k |
1.323 |
2.072 |
2.706 |
5.024 |
6.635 |
7.879 |
某单位为了制定节能减排的目标,先调查了用电量 (度)与气温
(度)与气温 (℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
由表中数据,得线性回归方程 ,则
,则 = .
= .
在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线 上,则这组样本数据的样本相关系数为 .
上,则这组样本数据的样本相关系数为 .
某商场在销售过程中投入的销售成本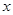 与销售额
与销售额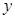 的统计数据如下表:
的统计数据如下表:
| 销售成本x(万元) |
3 |
4 |
6 |
7 |
销售额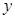 (万元) (万元) |
25 |
34 |
49 |
56 |
根据上表可得,该数据符合线性回归方程: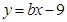 .由此预测销售额为100万元时,投入的销售成本大约为 ;
.由此预测销售额为100万元时,投入的销售成本大约为 ;
某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
| x |
18 |
13 |
10 |
-1 |
| y |
25 |
34 |
39 |
62 |
由表中数据得线性回归方程y=-2x+a,预测当气温为-4 ℃时,用电量的度数约为 .
某次测量发现一组数据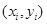 具有较强的相关性,并计算得
具有较强的相关性,并计算得  ,其中数据
,其中数据 ,Y)因书写不清,只记得
,Y)因书写不清,只记得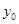 是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
已知x,Y之间的数据如下表所示,则Y与x之间的线性回归直线一定过点________.
| x |
1.08 |
1.12 |
1.19 |
1.28 |
| Y |
2.25 |
2.37 |
2.40 |
2.55 |
试题篮
()