高中数学变量间的相关关系填空题

某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表。为了检验主修统计专业是否与性别有关系，根据表中的数据，得到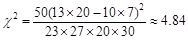
因为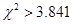，所以断定主修统计专业与性别有关系，这种判断出错的可能性为   。

专业 性别	非统计专业	统计专业
男	13	10
女	7	20

 

下表是我市某厂～月份用水量（单位：百吨）的一组数据：

月份
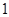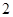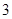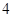用水量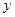

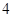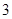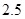由散点图可知，用水量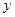与月份之间有较好的线性相关关系，其线性回归直线方程是，则___________．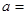

某公司的广告费支出x与销售额y（单位：万元）之间有下列对应数据：由资料显示对呈线性相关关系。

x	2	4	5	6	8
y	30	40	60	50	70

根据上表提供的数据得到回归方程中的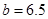，预测销售额为115万元时约需万元广告费       

在求两个变量x和y的线性回归方程过程中, 计算得="25," ="250," ="145," ="1380," 则该回归方程是                   .

某产品广告费用x与销售额y的统计数据如下表：

广告费用x（万元）	4	2	3	5
销售额y(万元)	49	26	39	54

根据上表可得回归直线方程中的为9.4，据此模型预报广告费用为6万元时销售额为      .

某研究小组为了研究中学生的身体发育情况，在某学校随机抽出20名15至16周岁的男生，将他们的身高和体重制成2×2的列联表，根据列联表的数据，可以有       %的把握认为该学校15至16周岁的男生的身高和体重之间有关系.

	超重	不超重	合计
偏高	4	1	5
不偏高	3	12	15
合计	7	13	20

下表是某厂1-4月份用水量(单位:100t)的一组数据, 由其散点图可知, 用水量y与月份x之间有较好的线性相关关系,其线性回归方程是_________________.

月份x	1	2	3	4
用水量y(100t)	4.4	4	3	2.5

．已知x与y之间的一组数据：

x	0	1	2	3
y	1	3	5	7

则y与x的线性回归方程y=bx+a必过点　　　　　　 （填写序号)
①（2，2）            ②（1.5，0）     ③（1.5，4）  ④ (1,  2)

小华的妈妈经营一家饮品店，经常为进货数量而烦恼，于是小华
代妈妈进行统计，其中某种饮料的日销售量y（瓶）与当天的气温x（℃）的几组对照数据
如下：

x	10	15	20	25	30
y	110	125	160	185	220

根据上表得回归方程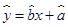中的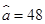，据此模型估计当气温为35℃时，该饮料的日销售量为          瓶.

已知x与y之间的一组数据：

则y与x的线性回归方程为y=bx+a必过点__________________。

、某服装商场为了了解毛衣的月销售量y (件)与月平均气温x(℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：

月平均气温x(℃)	17	13	8	2
月销售量y(件)	24	33	40	55

由表中数据算出线性回归方程中的，气象部门预测下个月的平均气温约为6℃，据此估计，该商场下个月毛衣的销售量约为________件．

高三某学生高考成绩与高三期间有效复习时间（天）正相关，且回归方程是，若期望他高考达到560分，那么他的有效复习时间应不低于______天．

调查了某地若干户家庭的年收入x（单位：万元）和年饮食支出y（单位：万元），调查显示年收入x与年饮食支出y具有线性相关关系，并由调查数据得到y对x的回归直线方程：.由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加____________万元.

调查了某地若干户家庭的年收入x（单位：万元）和年饮食支出y（单位：万元），调查显示年收入x与年饮食支出y具有线性相关关系，并由调查数据得到y对x的回归直线方程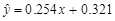：.由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加____________万元.

在吸烟与患肺病这两个分类变量的计算中，若从统计量中求出有95%的把握认为“吸烟与患肺病有关系”，是指有         的可能性使得推判出现错误.