高中数学变量间的相关关系试题

．有五组变量：①汽车的重量和汽车每消耗1升汽油所行驶的平均路程；②平均日学习时间和平均学习成绩；③某人每日吸烟量和其身体健康情况；④正方形的边长和面积；⑤汽车的重量和百公里耗油量.其中两个变量成正相关的是            (     )   
A．①③     B．②④     C．②⑤      D．④⑤

为了判断高中三年级学生选修文科是否与性别有关，现随机抽取50名学生，
得到如下22联表：

	理科	文科
男	13	10
女	7	20

根据表中的数据，则认为选修文科与性别有关出错的可能性为       ．

在回归分析中，代表了数据点和它在回归直线上相应位置的差异的是（）
Ａ．总偏差平方和   Ｂ．残差平方和  C．回归平方和    Ｄ．相关指数

下列结论正确的是（　　）
①函数关系是一种确定性关系；②相关关系是一种非确定性关系；③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法．

A．①②

B．①②③

C．①②④

D．①②③④

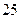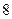(本题满分12分)班主任为了对本班学生的考试成绩进行分析，决定从全班位女同学， 位男同学中随机抽取一个容量为的样本进行分析。
（Ⅰ）如果按性别比例分层抽样，可以得到多少个不同的样本（只要求写出算式即可，不必计算出结果）；
（Ⅱ）随机抽取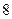位同学，数学成绩由低到高依次为：；
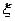物理成绩由低到高依次为：，若规定分（含分）以上为优秀，记为这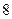位同学中数学和物理分数均为优秀的人数，求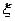的分布列和数学期望；
（Ⅲ）若这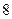位同学的数学、物理分数事实上对应下表：

学生编号
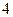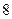数学分数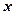
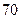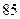物理分数

 
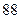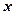
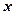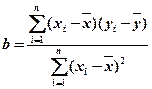根据上表数据可知，变量与之间具有较强的线性相关关系，求出与的线性回归方程（系数精确到）．（参考公式：，其中，； 参考数据：，，，，，，）

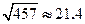线性回归方程表示的直线必定过         （   ） 

A．（0，0）点

B．（，0）点

C．（，0）点

D．（，）点

某车间为了规定工时定额，需要确定加个某零件所花费的时间，为此作了四次实验，得到的数据如下：

零件的个数x(个)	2	3	4	5
加工的时间y(小时)	2.5	3	4	4.5

（1）  求出y关于x的线性回归方程；
（2）  试预测加工10个零件需要多少时间？

在对两个变量x,y进行线性回归分析时有以下步骤：
（1）利用回归方程进行预测；
（2）收集数据；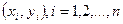
（3)求线性回归方程；
（4）根据所收集的数据绘制散件图.
则正确的操作顺序是____________

下表是某厂1到4月份用水量情况（单位：百吨）的一组数据

月份x	1	2	3	4
用水量y	4.5	4	3	2.5

用水量y与月份x之间具有线性相关关系，其线性回归方程为,则a的值为（ ）

A．5.25

B．

C．2.5

D．3.5

已知x与y之间的一组数据

x	0	1	2	3
y	1	3	5	7

(1)画出散点图
（2）若x与y线性相关，写出线性回归方程必定经过的点
（3）若x与y线性相关求出线性回归方程，
（4）说出2个刻画回归效果的手段，假设R=0.74说明什么问题。
参考公式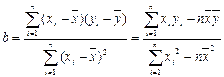

设有一个回归直线方程，则变量x增加1个单位时

A．y平均增加1.5个单位	B．y平均增加2个单位
C．y平均减少1.5个单位	D．y平均减少2个单位

儿子的身高和父亲的身高是：                         

A．确定性关系

B．相关关系

C．函数关系

D．无任何关系

若一函数模型为，将转化为的线性回归方程，需做变换＝

A．

B．

C．

D．以上都不对

（实验班）线性回归方程表示的直线＝a＋bx，必定过(　　)

A．(0,0)点

B．(，)点

C．(0，)点

D．(，0)点

．已知关于的回归方程为，则变量减少一个单位时（ ）

A．平均增加1.5个单位	B．平均增加2个单位
C．平均减少1.5个单位	D．平均减少2个单位