高中数学变量间的相关关系试题

下面哪些变量是相关关系（     ）

A．出租车费与行驶的里程	B．房屋面积与房屋价格
C．身高与体重	D．铁的大小与质量

已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是(   )

A．=1.23x＋4

B．="1.23x+5"

C．="1.23x+0.08"

D．=0.08x+1.23

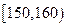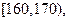
随机抽取某中学甲、乙两个班各10名同学，测量他们的身高（单位：cm）获得身高数据的茎叶图如下图甲，在样本的20人中，记身高在，的人数依次为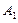、、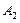、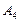．图乙是统计样本中身高在一定范围内的人数的算法流程图，由图甲可知甲、乙两班中平均身高较高的是     班；图乙输出的 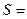        ．（用数字作答）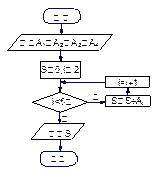

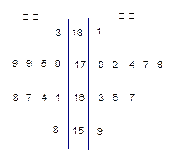
图甲                                  图乙

（本小题满分12分）在调查的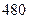名上网的学生中有名学生睡眠不好,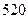名不上网的学生中有名学生睡眠不好,利用独立性检验的方法来判断是否能以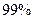的把握认为“上网和睡眠是否有关系”.
附：；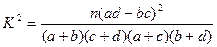
参考数据

，.

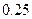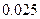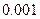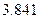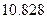随机抽取某中学甲乙两班各6名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图. 则甲班样本数据的众数和乙班样本数据的中位数分别是

A．170，170

B．171，171

C．171，170

D．170，172

（本小题满分12分）
某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如图所示的茎叶图表示．
（Ⅰ）求甲、乙两名运动员得分的中位数；
（Ⅱ）你认为哪位运动员的成绩更稳定？
（Ⅲ）如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分，求甲的得分大于乙的得分的概率．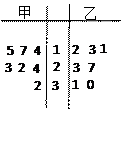

某商品销售量y（件）与销售价格x（元/件）负相关，则其回归方程可能是     （   ）

A．	B．
C．	D．

图1是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，则甲、乙两人这几场比赛得分的中位数之和是

A．65	B．64
C．63	D．62

甲、已乙两名篮球运动员每场比赛的得分情况用茎叶图表示如下：则下列说法中正确的个数为         
⑴甲得分的中位数为26，乙得分的中位数为36；
⑵甲、乙比较，甲的稳定性更好；
⑶乙有的叶集中在茎3上
⑷甲有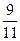的叶集中在茎1、2、3上。

A．1

B．2

C．3

D．4

回归分析中，代表了数据点和它在回归直线上相应位置的差异的是（      ）

A．总偏差平方和

B．残差平方和

C．回归平方和

D．相关指数R^2

以下结论不正确的是                                        （    ）

A．根据2×2列联表中的数据计算得出K^2≥6.635, 而P（K^2≥6.635）≈0.01，则有99%的把握认为两个分类变量有关系

B．在线性回归分析中，相关系数为r，|r|越接近于1，相关程度越大；|r| 越小，相关程度越小

C．在回归分析中，相关指数R^2越大，说明残差平方和越小，回归效果越好

D．在回归直线中，变量x=200时，变量y的值一定是15

已知x与y之间的一组数据：   

x	0	1	2	3
y	1	3	5	7

则y与x的线性回归方程为=必过                                                     （   ）

A．点

B．点

C．点

D．点

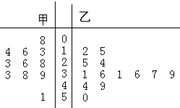
由于当前学生课业负担较重，造成青少年视力普遍下降，现从某高中随机抽取16名学生，经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎，小数点后的一位数字为叶)如下：

（Ⅰ）指出这组数据的众数和中位数；
（Ⅱ）若视力测试结果不低丁5.0，则称为“好视力”，求校医从这16人中随机选取3人，至多有1人是“好视力”的概率；
（Ⅲ）以这16人的样本数据来估计整个学校的总体数据，若从该校(人数很多)任选3人，记表示抽到“好视力”学生的人数，求的分布列及数学期望．

对变量x, y 有观测数据（，）（i=1,2,…，10），得散点图1；对变量u ，v 有观测数据（，）（i=1,2,…，10）,得散点图2. 由这两个散点图可以判断。

图1                           图2

A．变量x 与y 正相关，u 与v 正相关	B．变量x 与y 正相关，u 与v 负相关
C．变量x 与y 负相关，u 与v 正相关	D．变量x 与y 负相关，u 与v 负相关

甲乙丙丁四位同学各自对两变量的线性相关性进行分析，并用回归分析方法得到相关系数与残差平方和，如右表则哪位同学的试验结果体现两变量更强的线性相关性（   ）

	甲	乙	丙	丁

 
A 甲            B 乙          C 丙          D 丁