如图是2010年我校主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和中位数分别为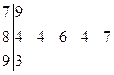
A. ,84 ,84 |
B. ,86 ,86 |
C.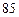 ,84 ,84 |
D.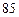 ,86 ,86 |
某校为提高教学质量进行教改实验,设有试验班和对照班.经过两个月的教学试验,进行了一次检测,试验班与对照班成绩统计如右边的 列联表所示(单位:人),则其中
列联表所示(单位:人),则其中 ,
, .
.
| |
80及80分以下 |
80分以上 |
合计 |
| 试验班 |
32 |
18 |
50 |
| 对照班 |
12 |
 |
50 |
| 合计 |
44 |
56 |
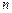 |
在相关分析中,对相关系数 ,下列说法正确的是
,下列说法正确的是
A. 越大,线性相关程度越强 越大,线性相关程度越强 |
B. 越小,线性相关程度越强 越小,线性相关程度越强 |
C. 越大,线性相关程度越弱, 越大,线性相关程度越弱, 越小,线性相关程度越强 越小,线性相关程度越强 |
D. 且 且 越接近 越接近 ,线性相关程度越强, ,线性相关程度越强, 越接近 越接近 ,线性相关程度越弱 ,线性相关程度越弱 |
某饮料店的日销售收入y(单位:百元)与当天平均气温x(单位:°C)之间有下列数据:
| x |
-2 |
-1 |
0 |
1 |
2 |
| y |
5 |
4 |
2 |
2 |
1 |
甲,乙,丙三位同学对上述数据进行了研究,分别得到了x与y之间的三个线性回归议程①=-x+2.8;②=-x+3;③=-1.2x+2.6,其中正确的是________;
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1) 请画出上表数据的散点图;
(2) 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(附:最小二乘法求线性回归方程系数公式  ,
,
另外:计算数据3×2.5+4×3+5×4+6×4.5=66.5可供使用)
(3) 已知该厂技术改造前100吨甲产品能耗为90吨标准煤;试根据(2)所求出的线性回归方程,预测生产 100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
废品率x%和每吨生铁成本y(元)之间的回归直线方程为y=256+3x,表明( )
| A.废品率每增加1%,生铁成本增加259元. | B.废品率每增加1%,生铁成本增加3元. |
| C.废品率每增加1%,生铁成本每吨增加3元. | D.废品率不变,生铁成本为256元. |
在下列各图中,每个图的两个变量具有相关关系的图是







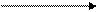
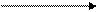
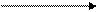
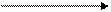 (1) (2) (3) (4)
(1) (2) (3) (4)
| A.(1)(2) | B.(1)(3) | C.(2)(4) | D.(2)(3) |
刻画数据的离散程度的度量,下列说法正确的是
(1) 应充分利用所得的数据,以便提供更确切的信息;可以用多个数值来刻画数据的离散程度;对于不同的数据集,其离散程度大时,该数值应越小。
| A.(1)和(3) | B.(2)和(3) | C.(1)和(2) | D.都正确 |
改革开放30年以来,我国高等教育事业迅速发展,对我省1990~2000年考大学升学百分比分城市、县镇、农村进行统计,将1990~2000年依次编号为0~10,回归分析之后得到每年考入大学的百分比y与年份x的关系为:
城市: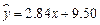 ; 县镇:
; 县镇: ;农村:
;农村: .
.
根据以上回归直线方程,城市、县镇、农村三个组中, 的大学入学率增长最快 . 按同样的增长速度,可预测2010年,农村考入大学的百分比为 %.
. 按同样的增长速度,可预测2010年,农村考入大学的百分比为 %. 
五四青年节歌咏比赛上,七位评委为某选手打出的分数的茎叶统计图如右,去掉一个最高分和一个最低分后,所剩数据的平均数和方差 分别为
分别为
A. , , |
B. , , |
C. , , |
D. , , |
已知两个变量x,y具有线性相关关系,并测得(x,y)的四组值分别是(2,3)、
(5,7)、(8,9)、(11,13),则求得的线性回归方程所确定的直线必定经过点
A (2,3) B (8,9) C (11,13) D (6.5,8)
四个学习小组分别对不同的变量组(每组为两个变量)进行该组两变量间的线性相关作实验,并用回归分析的方法分别求得相关系数 与方差
与方差 如下表所示,其中哪个小组所研究的对象(组内两变量)的线性相关性更强
如下表所示,其中哪个小组所研究的对象(组内两变量)的线性相关性更强
| A.第一组 | B.第二组 |
| C.第三组 | D.第四组 |
试题篮
()