对于线性相关系数
叙述正确的是（ ）
A． ，且越大，相关程度越大. |
B．，且 越大，相关程度越大. |
C． ，且越大，相关程度越大. |
| D．，且越大，相关程度越大. |
设对变量x,y有如下观察数据:
| x |
-2.0 |
0.6 |
1.4 |
1.3 |
0.7 |
4.0 |
| y |
-6 |
-2 |
7 |
6 |
-1 |
14 |
则y对x的回归直线
必过定点________.
在2010年3月15日那天，龙岩市物价部门对本市5家商场某商品的一天销售量及其价格进行调查，5家商场的售价
元和销售量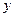
件之间的一组数据如右表所示，由散点图可知，销售量y与价格之间有较好的线性相关关系，若其线性回归直线方程是：
，(参考公式：回归方程；
)，则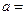
___________。
| 价格 |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量 |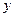
11 |
10 |
8 |
6 |
5 |
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：
| 日期 |
1月10日 |
2月10日 |
3月10日 |
4月10日 |
5月10日 |
6月10日 |
昼夜温差 |
10 |
11 |
13 |
12 |
8 |
6 |
就诊人数 （个） |
22 |
25 |
29 |
26 |
16 |
12 |
该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验。
（Ⅰ）求选取的2组数据恰好是相邻两个月的概率；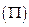
若选取的是1月与6月的两组数据，请根据2至5月份的数据，求出y关于x的线性回归方程
；
（Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？
（参考数据：11×25+13×29+12×26+8×16=1092，
）
下列命题中,其中假命题是 ( )
A．对分类变量X与Y的随机变量 的观测值 来说，越小，“X与Y有关系”可信程度越大 |
| B．用相关系数r来刻画回归的效果时，|r|的值越大，说明模型拟合的效果越好 |
C．回归直线恒过定点 |
| D．在研究事件A,B是有关时，当<3.841时，认为事件A与B是无关的。 |
下列有关样本相关系数的说法不正确的是
A．相关系数用来衡量变量 与 之间的线性相关程度 |
B． ，且 越接近于1，相关程度越大 |
| C．，且越接近于0，相关程度越小 |
D． ，且越接近于1，相关程度越大 |
为了探究患慢性气管炎与吸烟有无关系,调查了却
名
岁以上的人,结果如下表所示,据此数据请问:岁以上的人患慢性气管炎与吸烟习惯有关系吗?
| |
患慢性气管炎 |
未患慢性气管炎 |
合计 |
| 吸烟 |
43 |
162 |
205 |
| 不吸烟 |
13 |
121 |
134 |
| 合计 |
56 |
283 |
339 |
某人5次上班途中所花的时间（单位：分钟）分别为x，y，10，11，9。已知这组数据的平均数为10，方差为2，则|x-y|的值为 （ ）
| A．1 | B．2 | C．3 | D．4 |
试题篮
()
粤公网安备 44130202000953号
若
则
（ ）
的取值如下表所示：
，则
(B)
(C)
(D)
最小
最小
最
最小
( ).
，计算出
的值，则拒绝
当气温为-4°C时，预测用电量的度数约为