下表是某小卖部一周卖出热茶的杯数与当天气温的对比表:
| 气温/℃ |
18 |
13 |
10 |
4 |
-1 |
| 杯数 |
24 |
34 |
39 |
51 |
63 |
若热茶杯数y与气温x近似地满足线性关系,则其关系式最接近的是( )
| A.y="x+6" | B.y="-x+42" | C.y="-2x+60" | D.y=-3x+78 |
对于两个变量之间的相关系数,下列说法中正确的是( )
A. , ,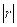 越大,相关程度越大, 越大,相关程度越大, 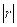 越小,相关程度越小 越小,相关程度越小 |
B. , ,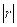 越大,相关程度越小, 越大,相关程度越小,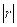 越小,相关程度越大 越小,相关程度越大 |
C.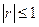 且 且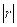 越接近于 越接近于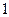 ,相关程度越大; ,相关程度越大;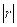 越接近于 越接近于 ,相关程度越小 ,相关程度越小 |
D.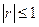 且 且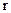 >0比 >0比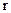 <0相关程度大; <0相关程度大; |
某10名同学的数学、物理、语文成绩如下表:
| 数学 |
136 |
125 |
122 |
87 |
108 |
113 |
111 |
70 |
94 |
74 |
| 物理 |
107 |
91 |
92 |
76 |
93 |
85 |
82 |
78 |
78 |
73 |
| 语文 |
86 |
114 |
104 |
109 |
100 |
106 |
112 |
104 |
95 |
99 |
试分别研究他们的数学成绩与物理成绩的关系、数学成绩与语文成绩的关系,你能发现什么规律?
在通过国家司法考试的考生中,统计发现重点大学理工科非法律专业的考生占了一定的比例,说明严密的逻辑思维与法律专业的理解学习存在什么关系( ).
| A.正相关 | B.负相关 | C.无相关 | D.不确定 |
在通过国家司法考试的考生中,统计发现重点大学理工科非法律专业的考生占了一定的比例,说明严密的逻辑思维与法律专业的理解学习存在什么关系( ).
| A.正相关 | B.负相关 | C.无相关 | D.不确定 |
数据x1,x2, …,x8的平均数为6,标准差为2,则数据2x1-6,2x2-6, …,2x8-6的平均数为___________,方差为_________.
两个具有线性相关关系的变量的一组数据为:
| 数据 |
1 |
2 |
3 |
… |
n |
| 变量x |
x1 |
x2 |
x3 |
… |
xn |
| 变量y |
y1 |
y2 |
y3 |
… |
yn |
将以上数据,以x为自变量,y为因变量,得回归方程为 =bx+a;将y为自变量,x为因变量,得回归方程为
=bx+a;将y为自变量,x为因变量,得回归方程为 =b′y+a′.
=b′y+a′.
定义两个变量的相关关系数r的计算公式为r= ,它可表示两个变量线性关系的强弱.
,它可表示两个变量线性关系的强弱.
试问r能否用上述两方程中的b,a与b′,a′表示?如能,怎样表示?
日常生活中,某些东西所含的热量比较高,对我们的身体有一定的影响,下表给出了不同类型八种饼干的数据,第一列数据表示八种饼干各含热量的百分比,第二列数据表示顾客对八种饼干所给予分数(百分制).
| 品种 |
所含热量的百分比 |
口味记录 |
| 1 |
25 |
89 |
| 2 |
34 |
89 |
| 3 |
20 |
80 |
| 4 |
19 |
78 |
| 5 |
26 |
75 |
| 6 |
20 |
71 |
| 7 |
19 |
65 |
| 8 |
24 |
62 |
(1)作出这些数据的散点图;
(2)求出回归直线;
(3)关于两个变量之间的关系,你能得出什么结论?
(4)为什么人们更喜欢吃位于回归直线上方的饼干而不是下方的饼干?
为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立地做了10次试验和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2,已知两个人在试验中发现对变量x的观测数据的平均数都为s,对变量y的观测数据平均数都为t,那么下列说法正确的是( )
| A.l1和l2有交点(s,t) | B.l1和l2相交,但交点不一定是(s,t) |
| C.l1和l2必平行 | D.l1和l2必重合 |
判断下列关系是否为相关关系:
(1)历史上,有人认为人们的着装与经济好坏有关系,着装越鲜艳,经济越景气,你认为着装与经济真的有这种相关关系吗?
(2)下面是6位同学的身高与体重的数据表:
| 身高(cm) |
168 |
173 |
176 |
179 |
181 |
185 |
| 体重(kg) |
56 |
59 |
60 |
65 |
64 |
68 |
画出散点图,并判断它们是否有相关关系.
测得某国家10对父子身高(单位:英寸)如下:
| 父亲身高(x) |
60 |
62 |
64 |
65 |
66 |
67 |
68 |
70 |
72 |
74 |
| 儿子身高(y) |
63.6 |
65.2 |
66 |
65.5 |
66.9 |
67.1 |
67.4 |
68.3 |
70.1 |
70 |
(1)对变量y与x进行相关性检验;
(2)如果y与x之间具有线性相关关系,求回归直线方程;
(3)如果父亲的身高为73英寸,估计儿子的身高.
某地10户家庭的年收入和年饮食支出的统计资料如下表:
| 年收入 x(万元) |
2 |
4 |
4 |
6 |
6 |
6 |
7 |
7 |
8 |
10 |
| 年饮食支出 y(万元) |
0.9 |
1.4 |
1.6 |
2.0 |
2.1 |
1.9 |
1.8 |
2.1 |
2.2 |
2.3 |
(1)根据表中数据,确定家庭的年收入和年饮食支出之间是否具有相关关系;若具有相关关系求出y与x的回归直线方程;
(2)如果某家庭年收入为9万元,预测其年饮食支出.
某公司利润y与销售总额x(单位:千万元)之间有如下对应数据:
| x |
10 |
15 |
17 |
20 |
25 |
28 |
32 |
| y |
1 |
1.3 |
1.8 |
2 |
2.6 |
2.7 |
3.3 |
(1)画出散点图;
(2)求回归直线方程;
(3)估计销售总额为24千万元时的利润.
试题篮
()