[2013·怀柔模拟]某中学2013年共91人参加高考,统计数据如下:
| |
城镇考生 |
农村考生 |
| 录取 |
31 |
24 |
| 未录取 |
19 |
17 |
则考生的户口形式和高考录取的关系是________.(填无关、多大把握有关)
[2013·福建高考]已知x与y之间的几组数据如下表:
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程为 =
= x+
x+ .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
A. >b′,
>b′, >a′ B.
>a′ B. >b′,
>b′, <a′
<a′
C. <b′,
<b′, >a′ D.
>a′ D. <b′,
<b′, <a′
<a′
已知两个变量x,y之间具有线性相关关系,试验测得(x,y)的四组值分别为(1,2),(2,4),(3,5),(4,7),则y与x之间的回归直线方程为( )
| A.y=0.8x+3 | B.y=-1.2x+7.5 |
| C.y=1.6x+0.5 | D.y=1.3x+1.2 |
下列五个命题
①任何两个变量都具有相关关系 ②圆的周长与该圆的半径具有相关关系
③某商品的需求量与该商品的价格是一种非确定性关系
④根据散点图求得的回归直线方程可能是没有意义的
⑤两个变量间的相关关系可以通过回归直线,把非确定性问题转化为确定性问题进行研究
正确命题的序号为____________.
设有一个直线回归方程为 ,则变量
,则变量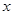 增加一个单位( )
增加一个单位( )
| A.y平均增加 1.5 个单位 |
| B.y 平均增加 2 个单位 |
| C.y 平均减少 1.5 个单位 |
| D.y 平均减少 2 个单位 |
设某中学的女生体重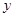 (kg)与身高
(kg)与身高 (cm)具有线性相关关系,根据一组样本数
(cm)具有线性相关关系,根据一组样本数
 ,用最小二乘法建立的线性回归直线方程为
,用最小二乘法建立的线性回归直线方程为 ,给出下列结论,则错误的是( )
,给出下列结论,则错误的是( )
A.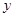 与 与 具有正的线性相关关系 具有正的线性相关关系 |
| B.若该中学某女生身高增加1cm,则其体重约增加0.85kg |
C.回归直线至少经过样本数据  中的一个 中的一个 |
D.回归直线一定过样本点的中心点 |
根据如下样本数据
| 3 |
4 |
5 |
6 |
7 |
8 |
|
| 4.0 |
2.5 |
-0.5 | 0.5 |
-2.0 | -3.0 |
得到的回归方程为,则()
| A. |
|
B. |
|
C. |
|
D. |
|
某人摆一个摊位卖小商品,一周内出摊天数x与盈利y(百元),之间的一组数据关系见表:
 |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
已知 ,
, ,
,
(1)在下面坐标系中画出散点图;
(2)计算 ,
, ,并求出线性回归方程;
,并求出线性回归方程;
(3)在第(2)问条件下,估计该摊主每周7天要是天天出摊,盈利为多少?
某产品的广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
58 |
根据上表可得回归方程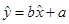 中的
中的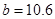 ,据此模型预报广告费用为
,据此模型预报广告费用为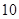 万元时销售额为( ).
万元时销售额为( ).
A.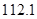 万元 B.
万元 B.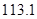 万元 C.
万元 C. 万元 D.
万元 D.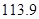 万元
万元
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程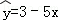 ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程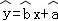 必过(
必过( );
);
④在一个2×2列联中,由计算得K2=13.079则有99%的把握确认这两个变量间有关系;
其中错误 的个数是( ).
本题可以参考独立性检验临界值表:
| P(K2≥k) |
0.5 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.25 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.535 |
7.879 |
10.828 |
A.0 B.1 C.2 D.3
如果随机变量ξ~B(n,p),且Eξ=7,Dξ=6,则P等于_________ .
设某大学的女生体重 (单位:kg)与身高
(单位:kg)与身高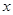 (单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 ,则下列结论中不正确的是 ( )
,则下列结论中不正确的是 ( )
A. 与 与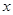 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心( , , ) ) |
| C.若该大学某女生身高增加1cm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
已知某企业上半年前5个月产品广告投入与利润额统计如下:
| 月份 |
1 |
2 |
3 |
4 |
5 |
| 广告投入(x万元) |
9.5 |
9.3 |
9.1 |
8.9 |
9.7 |
| 利润(y万元) |
92 |
89 |
89 |
87 |
93 |
由此所得回归方程为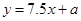 ,若6月份广告投入10(万元)估计所获利润为( )
,若6月份广告投入10(万元)估计所获利润为( )
A.95.25万元 B.96.5万元 C.97万元 D.97.25万元
某车间加工零件的数量 与加工时间
与加工时间 的统计如下表:
的统计如下表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程 中的值
中的值 为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( ).
为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( ).
A.84分钟 B.94分钟 C.102分钟 D.112分钟
根据下表所示的统计资料,求出了y关于x的线性回归方程为 =1.23x+0.08,则统计表中t的值为( )
=1.23x+0.08,则统计表中t的值为( )
| x |
2 |
3 |
4 |
5 |
6 |
| y |
2.2 |
3.8 |
t |
6.5 |
7.0 |
A.5.5 B.5.0 C.4.5 D.4.8
试题篮
()