有人收集了春节期间平均气温x(℃)与某取暖商品销售额y(万元)的有关数据(x,y)分别为:(﹣2,20),(﹣3,23),(﹣5,27),(﹣6,30),根据以上数据,用线性回归的方法,求得销售额y与平均气温x之间线性回归方程y=bx+a的系数b=﹣2.4,则预测平均气温为﹣8℃时该商品的销售额为_________ 万元.
某产品的广告费用支出 (万元)与产品销售额
(万元)与产品销售额 (万元)之间的统计数据如下:
(万元)之间的统计数据如下:
广告费用支出 (万元) (万元) |
2 |
4 |
5 |
6 |
8 |
产品销售额 (万元) (万元) |
30 |
40 |
60 |
50 |
70 |
求得回归直线方程为 ,若投入
,若投入 万元的广告费用,估计销售额为
万元的广告费用,估计销售额为
(A)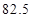 万元 (B)
万元 (B) 万元(C)
万元(C)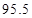 万元 (D)
万元 (D) 万元
万元
给出下列四个结论:
①若 组数据
组数据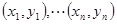 的散点都在
的散点都在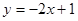 上,则相关系数
上,则相关系数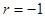 ;
;
②由直线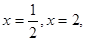 曲线
曲线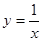 及
及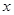 轴围成的图形的面积是
轴围成的图形的面积是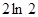 ;
;
③已知随机变量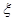 服从正态分布
服从正态分布
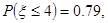 则
则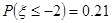 ;
;
④设回归直线方程为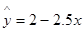 ,当变量
,当变量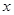 增加一个单位时,
增加一个单位时, 平均增加2个单位.
平均增加2个单位.
其中正确结论的个数为
A.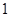 |
B.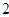 |
C.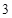 |
D.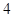 |
某产品的广告费用x与销售额y的统计数据如表:
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程 ,其中
,其中 =9.4,据此模型预报广告费用为6万元时,销售额为 ( ).
=9.4,据此模型预报广告费用为6万元时,销售额为 ( ).
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
已知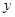 与
与 之间具有很强的线性相关关系,现观测得到
之间具有很强的线性相关关系,现观测得到 的四组观测值并制作了右边的对照表,由表中数据粗略地得到线性回归直线方程为
的四组观测值并制作了右边的对照表,由表中数据粗略地得到线性回归直线方程为 ,其中
,其中 的值没有写上.当
的值没有写上.当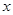 等于
等于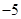 时,预测
时,预测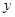 的值为 .
的值为 .
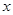 |
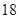 |
 |
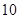 |
 |
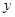 |
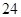 |
 |
 |
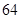 |
下面是两个变量的一组数据:
| X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
则这两个变量之间的线性回归方程是( )
A.y=-16+9x B.y=31-x C.y=30-x D.y=-15+9x
以下四个命题中
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②对于命题 :
: 使得
使得 . 则
. 则
 :
: 均有
均有 ;
;
③设随机变量  ,若
,若 ,则
,则 ;
;
④两个随机变量的线性相关性越强,则相关系数就越接近于1.
其中真命题的个数为[来
| A.1 | B.2 | C.3 | D.4 |
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是 ( )
A.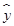 =-10x+200 =-10x+200 |
B.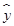 =10x+200 =10x+200 |
C.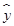 =-10x-200 =-10x-200 |
D.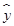 =10x-200 =10x-200 |
变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4)(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2)(13,1),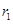 表示变量Y与X之间的线性相关系数,
表示变量Y与X之间的线性相关系数,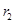 表示变量V与U之间的线性相关系数,则( )
表示变量V与U之间的线性相关系数,则( )
A.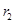 < <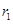 <0 <0 |
B.0<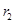 < <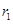 |
C.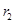 <0< <0<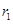 |
D.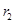 = =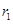 |
四名同学根据各自的样本数据研究变量 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
① 与
与 负相关且
负相关且 ;
;
② 与
与 负相关且
负相关且 ;
;
③ 与
与 正相关且
正相关且 ;
;
④ 与
与 正相关且
正相关且 .
.
其中一定不正确的结论的序号是()
| A.①② | B.②③ | C.③④ | D.①④ |
试题篮
()