下表是某厂1—4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归方程为 =-0.7x+a,则a等于( )
=-0.7x+a,则a等于( )
A.10.5 B.5.15 C.5.2 D.5.25
下列说法中正确的有( )
①若r>0,则x增大时,y也相应增大; ②若r<0,则x增大时,y也相应增大;
③若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个点均在一条直线上.
| A.①② | B.②③ | C.①③ | D.①②③ |
若变量 与
与 之间的相关系数
之间的相关系数 ,则变量
,则变量 与
与 之间
之间
| A.不具有线性相关关系 |
| B.具有线性相关关系 |
| C.它们的线性相关关系还需要进一步确定 |
| D.不确定 |
一个车间为了规定工作定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
由表中数据,求得线性回归方程 ,根据回归方程,
,根据回归方程,
预测加工70个零件所花费的时间为 分钟.
若变量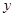 与
与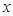 之间的相关系数
之间的相关系数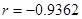 ,则变量
,则变量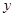 与
与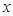 之间
之间
| A.不具有线性相关关系 |
| B.具有线性相关关系 |
| C.它们的线性相关关系还需要进一步确定 |
| D.不确定 |
在一次独立性检验中,有300人按性别和是否色弱分类如下表:
| |
男 |
女 |
| 正常 |
130 |
120 |
| 色弱 |
20 |
30 |
由此表计算得统计量K2=( ).
(参考公式: )
)
A.2 B.3 C.2.4 D.3.6
某单位为了了解用电量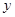 (度)与当天平均气温
(度)与当天平均气温 (°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程
(°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程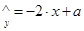 ,则
,则 __________.
__________.
平均气温 (°C) (°C) |
18 |
13 |
10 |
-1 |
用电量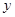 (度) (度) |
25 |
35 |
37 |
63 |
某工厂经过技术改造后,降低了能源消耗,经统计该厂某种产品的产量x(单位:吨)与相应的生产能耗y(单位:吨)有如下几组样本数据:
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
根据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得回归直线的斜率为0.7.已知该产品的年产量为10吨,则该工厂每年大约消耗的汽油为________吨.
若两个分类变量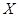 和
和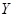 的
的 列联表为:
列联表为:
| |
 |
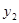 |
合计 |
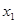 [ [ |
10 |
40 |
50 |
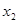 |
20 |
30 |
50 |
| 合计 |
30 |
70 |
100 |
参考公式:独立性检测中,随机变量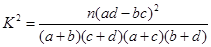
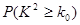 |
… |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
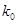 |
… |
2.706 |
3.841 |
5.0240 |
6.635 |
7.879 |
10.828 |
则认为“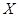 与
与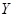 之间有关系”的把握可以达到 ( )
之间有关系”的把握可以达到 ( )
A. B.
B. C.
C.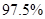 D.
D.
下列关于回归分析的说法正确的是 (填上所有正确说法的序号)
①相关系数 越小,两个变量的相关程度越弱;②残差平方和越大的模型,拟合效果越好;③用相关指数
越小,两个变量的相关程度越弱;②残差平方和越大的模型,拟合效果越好;③用相关指数 来刻画回归效果时,
来刻画回归效果时, 越小,说明模型的拟合效果越好;④用最小二乘法求回归直线方程,是寻求使
越小,说明模型的拟合效果越好;④用最小二乘法求回归直线方程,是寻求使 取最小值时的
取最小值时的 的值;⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
的值;⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
对具有线性相关关系的变量x、y有观测数据(xi,yi)(i=1,2,…,10),它们之间的线性回归方程是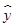 =3x+20,若
=3x+20,若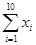 =18,则
=18,则 =________.
=________.
试题篮
()