高中数学变量间的相关关系试题

在线性回归模型中，下列说法正确的是(    )

A．是一次函数

B．因变量是由自变量唯一确定的

C．因变量除了受自变量的影响外，可能还受到其它因素的影响，这些因素会导致随机误差的产生

D．随机误差是由于计算不准确造成的，可以通过精确计算避免随机误差的产生

某单位为了了解用电量(千瓦时)与气温()之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：

气温()	18	13	10
用电量(千瓦时)	24	34	38	64

由表中数据得线性回归方程中，预测当气温为时，用电量约为(    )
A．58千瓦时  B．66千瓦时   C．68千瓦时  D．70千瓦时

已知x、y的取值如下表所示，若y与x线性相关，且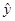＝0．95x＋，则＝____________．

x	0	1	3	4
y	2．2	4．3	4．8	6．7

 

两个变量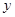与的回归模型中，分别选择了4个不同模型，它们的相关指数如下，其中拟合效果最好的模型是（ ）

A．模型1的相关指数为0.98	B．模型2的相关指数为0.80
C．模型3的相关指数为0.50	D．模型4的相关指数为0.25

某产品在某零售摊位的零售价x（单位：元）与每天的销售量y（单位：个）的统计资料如下表所示：由上表可得回归直线方程中的，据此模型预测零售价为15元时，每天的销售量为             ．

对相关系数r，下列说法正确的是

A．越大，线性相关程度越大

B．越小，线性相关程度越大

C．越大，线性相关程度越小，越接近0，线性相关程度越大

D．且越接近1，线性相关程度越大，越接近0，线性相关程度越小

已知与之间的一组数据为则与的回归直线方程必过定点_____． 

已知x,y的取值如下表所示，若y与x线性相关，且

x	0	1	3	4
	2．2	4．3	4．8	6．7

 
A．2．2          B．2．6     C．2．8       D．2．9

有下列关系：
①人的年龄与他（她）拥有的财富之间的关系；
②曲线上的点与该点的坐标之间的关系；
③苹果的产量与气候之间的关系；
④森林中的同一种树木，其横断面直径与高度之间的关系，
其中有相关关系的是(    )

A．①②③

B．①②

C．②③

D．①③④

人们在生活和消费过程中的过量碳排放，是造成全球气候变暖的重要因素之一，所谓“低碳生活”就是指生活作息时所耗用的能量要尽力减少，从而减低二氧化碳的排放量．某单位为了制定节能减排的目标，先调查了用电量（度）与气温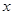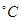（）之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：

气温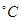（）	18	13	10
用电量（度）	24	34	38	64

 
由表中数据，得线性回归方程，当气温为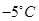时，预测用电量的度数约为           ．

根据如下样本数据：

	3	4	5	6	7	8
	4.0	2.5	-0.5	0.5	-2.0	-3.0

得到的回归方程为，则（   ）
A. ,        B. ,

C. ,        D. ,

已知变量 $x$与 $y$正相关，且由观测数据算得样本平均数 $\overline{x}=3,\overline{y}=3.5$，则由该观测的数据算得的线性回归方程可能是

A．	$\hat{y}=0.4x+2.3$	B．	$\hat{y}=2x-2.4$
C．	$\hat{y}=-2x+9.5$	D．	$\hat{y}=-0.3x+4.4$

某班主任对全班50名学生进行了作业量多少的调查，数据如下表：

	认为作业多	认为作业不多	总数
喜欢玩电脑游戏	18	9	27
不喜欢玩电脑游戏	8	15	23
总数	26	24	50

根据表中数据得到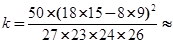5.059，因为p（K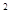≥5.024）=0.025,
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（ ）
（A）97.5%    （B） 95%      （C）90%       （D）无充分根据

某产品的广告费用x与销售额y的统计数据如表:

广告费用x(万元)	4	2	3	5
销售额y(万元)	49	26	39	54

 
根据上表可得回归方程，其中=9．4,据此模型预报广告费用为6万元时,销售额为　(　　)
A．63．6万元        B．65．5万元       C．67．7万元      D．72．0万元

调查了某地若干户家庭的年收x（单位：万元）和年饮食支出y（单位：万元），调查显示年收入x与年饮食支出y具有线性相关关系，井由调查数据得到y对x的回归直线方程．由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加      万元．