高中数学变量间的相关关系试题

（本小题满分12分）某地区2007年至2013年农村居民家庭纯收入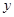（单位:千元）的数据如下表:

年份	2007	2008	2009	2010	2011	2012	2013
年份代号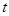	1	2	3	4	5	6	7
人均纯收入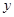	2.9	3.3	3.6	4.4	4.8	5.2	5.9

 
（Ⅰ）求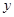关于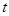的线性回归方程;（已知b=0.5）
（Ⅱ）利用（Ⅰ）中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.

（满分12分）假设关于某设备的使用年限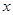和所支出的维修费用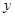（万元）有如下的统计资料：

使用年限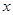
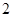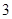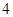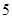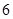维修费用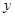

 
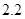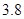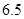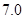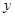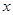若由资料知对呈线性相关关系。
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程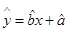的回归系数,．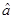
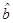（3）估计使用年限为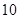年时，维修费用是多少？
，

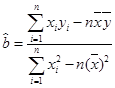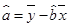
（满分12分）假设关于某设备的使用年限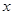和所支出的维修费用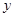（万元）有如下的统计资料：

使用年限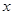
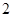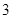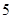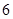维修费用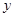

 
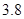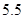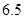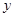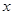若由资料知对呈线性相关关系。
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程的回归系数,．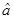
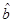（3）估计使用年限为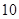年时，维修费用是多少？
，

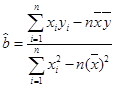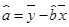
为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位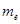数为，众数为，平均值为，则（ ）

A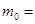．	B．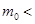
C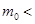．	D．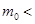

某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作四次试验，得到的数据如下：

零件的个数x（个）	2	3	4	5
加工的时间y（小时）	2．5	3	4	4．5

 
（1）已知零件个数与加工时间线性相关，求出y关于x的线性回归方程；
（2）试预测加工10个零件需要多少时间？

已知与之间的几组数据如下表:

X	0	1	2	3
y	1	3	5	7

 
则与的线性回归方程必过（   ）
A．           B．        C．         D．

观察下列关于两个变量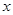和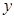的三个散点图，它们从左到右的对应关系依次为（  ）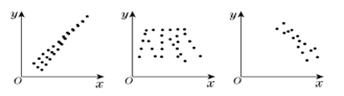

A．正相关、负相关、不相关	B．负相关、不相关、正相关
C．负相关、正相关、不相关	D．正相关、不相关、负相关

对具有线性相关关系的变量和，测得一组数据如下：

x	2	4	5	6	8
y	30	40	60	50	70

 
若已求得它们的回归方程的斜率为6．5，则这条直线的回归方程为                  ．

已知x，y的值如下表所示：

x	2	3	4
y	5	4	6

 
如果y与x呈线性相关且回归直线方程为，那么b=          .

下表数据是水温度x（℃）对黄酮延长性y（%）效应的试验结果，y是以延长度计算的，且对于给定的x，y为变量．

x（℃）	300	400	500	600	700	800
y（%）	40	50	55	60	67	70

 
（1）求y关于x的回归方程；
（2）估计水温度是1 000 ℃时，黄酮延长性的情况．
（可能用到的公式：，，其中、是对回归直线方程中系数、按最小二乘法求得的估计值）

四名同学根据各自的样本数据研究变量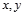之间的相关关系，并求得回归直线方程，分别得到以下四个结论：
①y与x负相关且；
②y与x负相关且；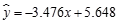
③y与x正相关且；
④y与x正相关且．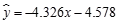
其中一定不正确的结论的序号是 （  ）

A．①②

B．②③

C．③④

D．①④

某市电力公司在电力供不应求时期，为了居民节约用电，采用“阶梯电价”方法计算电价，每月用电不超过度时，按每度元计费，每月用电超过度时，超过部分按每度元计费，每月用电超过度时，超过部分按每度元计费.
（1）设每月用电度，应交电费元，写出关于的函数；
（2）已知小王家第一季度缴费情况如下：

月份	1	2	3	合计
缴费金额	87元	62元	45元8角	194元8角

 
问：小王家第一季度共用了多少度电？

已知的取值如下表所示，若与线性相关，且，则（   ）

A．         B．        C．      D．[

某商品销售量（件）与销售价格（元/件）负相关，则其回归方程可能是（   ）

A．	B．
C．	D．

生产，两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：

测试指标
元件	8	12	40	32	8
元件	7	18	40	29	6

 
（Ⅰ）试分别估计元件、元件为正品的概率；
（Ⅱ）生产一件元件，若是正品可盈利50元，若是次品则亏损10元；生产一件元件，若是正品可盈利100元，若是次品则亏损20元，在（Ⅰ）的前提下
（i）求生产5件元件所获得的利润不少于300元的概率；   
（ii）记为生产1件元件和1件元件所得的总利润，求随机变量的分布列和期望．