如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是 ( ).

| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
下列四个命题中,正确命题的个数是( )个
① 若平面 平面
平面 ,直线
,直线 平面
平面 ,则
,则 ;
;
② 若平面 平面
平面 ,且平面
,且平面 平面
平面 ,则
,则 ;
;
③平面 平面
平面 ,且
,且 ,点
,点 ,
, ,若直线
,若直线 ,则
,则 ;
;
④直线 为异面直线,且
为异面直线,且 平面
平面 ,
, 平面
平面 ,若
,若 ,则
,则 .
.
A. |
B. |
C. |
D. |
[2014·深圳调研]如图,在四面体D-ABC中,若AB=CB,AD=CD,E是AC的中点,则下列正确的是( )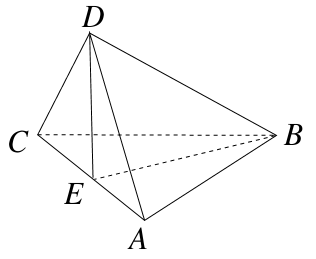
| A.平面ABC⊥平面ABD |
| B.平面ABD⊥平面BDC |
| C.平面ABC⊥平面BDE,且平面ADC⊥平面BDE |
| D.平面ABC⊥平面ADC,且平面ADC⊥平面BDE |
[2013·广东高考]设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( )
| A.若α⊥β,m⊂α,n⊂β,则m⊥n |
| B.若α∥β,m⊂α,n⊂β,则m∥n |
| C.若m⊥n,m⊂α,n⊂β,则α⊥β |
| D.若m⊥α,m∥n,n∥β,则α⊥β |
[2014·长春质检]如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为________.
[2014·福州质检]对于平面α和共面的直线m,n,下列命题是真命题的是( )
| A.若m,n与α所成的角相等,则m∥n |
| B.若m∥α,n∥α,则m∥n |
| C.若m⊥α,m⊥n,则n∥α |
| D.若m⊂α,n∥α,则m∥n |
[2013·安徽高考]在下列命题中,不是公理的是( )
| A.平行于同一个平面的两个平面相互平行 |
| B.过不在同一条直线上的三点,有且只有一个平面 |
| C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 |
| D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
已知三条不重合的直线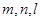 和两个不重合的平面
和两个不重合的平面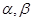 ,下列命题正确的是( )
,下列命题正确的是( )
A.若 , , ,则 ,则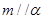 |
B.若 , ,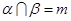 ,且 ,且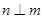 ,则 ,则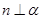 |
C.若 , , ,则 ,则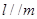 |
D.若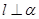 , , ,且 ,且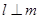 ,则 ,则 |
试题篮
()