已知集合A={直线},B={平面}, ,若
,若 ,给定下列命题:
,给定下列命题:
① ;②
;② ;③
;③ ;④
;④ .
.
其中一定正确的是( )
| A.①② | B.②③ | C.③④ | D.② |
在正四面体P—ABC中,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )
| A.BC//平面PDF | B.DF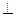 平面PAE 平面PAE |
C.平面PDF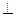 平面ABC 平面ABC |
D.平面PAE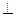 平面ABC 平面ABC |
已知两个平面垂直,下列命题 一个平面内已知直线必垂直于另一个平面内的任意一条直线.
一个平面内已知直线必垂直于另一个平面内的任意一条直线. 一个平面内的已知直线必垂直于另一个平面的无数条直线.
一个平面内的已知直线必垂直于另一个平面的无数条直线. 一个平面内的任一条直线必垂直于另一个平面.
一个平面内的任一条直线必垂直于另一个平面. 过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
其中正确的个数是( )
| A.3 | B.2 | C.1 | D.0 |
如图,在正方体ABCD—A1B1C1D1中,若E是AD的中点,则直线A1B与直线C1E的位置关系是( )w.
| A.平行 | B.相交 |
| C.共面 | D.垂直 |
试题篮
()