已知 为两条不同直线,
为两条不同直线, 为两个不同平面,给出下列命题: ( )
为两个不同平面,给出下列命题: ( )
①
②
③
④ ,
,
其中的正确命题序是( )
| A.②③ | B.③④ | C.①② | D.①②③④ |
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中( )

A.AB∥CD B.AB与CD相交
C.AB⊥CD D.AB与CD所成的角为60°
给出下面四个命题:
①“直线 直线
直线 ”的充要条件是“
”的充要条件是“ 平行于
平行于 所在的平面”;
所在的平面”;
②“直线 平面
平面 内所有直线”的充要条件是“
内所有直线”的充要条件是“ 平面
平面 ”;
”;
③“直线 ,
, 为异面直线”的充分而不必要条件是“直线
为异面直线”的充分而不必要条件是“直线 ,
, 不相交”;
不相交”;
④“平面 平面
平面 ”的必要而不充分条件是“
”的必要而不充分条件是“ 内存在不共线三点到
内存在不共线三点到 的距离相等”.
的距离相等”.
其中正确命题的序号是( )
| A.①② | B.②③ | C.③④ | D.②④ |
已知三个互不重合的平面 ,
, ,
, ,且
,且 ,
, ,
, ,给出下列命题:①
,给出下列命题:①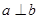 ,
, ,则
,则 ;
;
②若 ,则
,则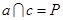 ;
;
③若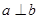 ,
, ,则
,则 ;
;
④ 若 ,则
,则 ,其中正确命题的个数为( )
,其中正确命题的个数为( )
| A.1 | B.2 | C.3 | D.4 |
(本小题满分12分)在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD 平面ABCD,
平面ABCD, ,
, .
.
(Ⅰ)求证:平面PCD 平面PAB;
平面PAB;
(Ⅱ)设E是棱AB的中点, ,
, ,求二面角
,求二面角 的余弦值.
的余弦值.
如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.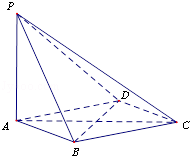
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)当平面PBC与平面PDC垂直时,求PA的长.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。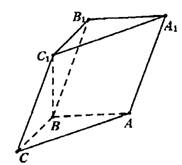
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设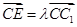 (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
若两个平面互相垂直,则下列命题中正确的是( )
| A.一个平面内的已知直线必垂直于另一个平面内的任意一条直线; |
| B.一个平面内的已知直线必垂直于另一个平面内的无数条直线; |
| C.一个平面内的任意一条直线必垂直于另一个平面; |
| D.过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面. |
有三个命题:
①垂直于同一个平面的两条直线平行;
②∀x∈R,x4>x2;
③命题“所有能被2整除的整数都是偶数”的否定是:所有能被2整除的整数都不是偶数.
其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
在正方体上任意选择4个顶点,由这4个顶点可能构成如下几何体:
①有三个面为全等的等腰直角三角形,有一个面为等边三角形的四面体;
②每个面都是等边三角形的四面体;
③每个面都是直角三角形的四面体;
④有三个面为不全等的直角三角形,有一个面为等边三角形的四面体.
以上结论其中正确的是________(写出所有正确结论的编号).
试题篮
()