如图所示,在正方体 中,点
中,点 是棱
是棱 上的一个动点,平面
上的一个动点,平面 交棱
交棱 于点
于点 .则下列命题中真命题的个数是( )
.则下列命题中真命题的个数是( )
①存在点 ,使得
,使得 //平面
//平面
②存在点 ,使得
,使得 平面
平面
③对于任意的点 ,平面
,平面 平面
平面
④对于任意的点 ,四棱锥
,四棱锥 的体积均不变
的体积均不变
| A.0个 |
| B.1个 |
| C.2个 |
| D.3个 |
已知 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , ,则 ,则 |
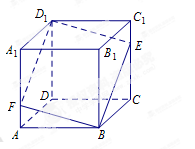
如图,在直四棱柱ABCD﹣A1B1C1D1中, E,F分别是AB,BC的中点,A1C1与B1D1交于点O.
(1)求证:A1,C1,F,E四点共面;
(2)若底面ABCD是菱形,且 A1E,求证:
A1E,求证: 平面A1C1FE.
平面A1C1FE.
如图, 是正方体
是正方体 的棱
的棱 的中点,给出下列命题
的中点,给出下列命题
①过 点有且只有一条直线与直线
点有且只有一条直线与直线 ,
, 都相交;
都相交;
②过 点有且只有一条直线与直线
点有且只有一条直线与直线 ,
, 都垂直;
都垂直;
③过 点有且只有一个平面与直线
点有且只有一个平面与直线 ,
, 都相交;
都相交;
④过 点有且只有一个平面与直线
点有且只有一个平面与直线 ,
, 都平行.其中真命题是:
都平行.其中真命题是:
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
如图,三棱柱 中,侧棱垂直底面,
中,侧棱垂直底面, 是棱
是棱 的中点.
的中点.
(1)证明:平面 ⊥平面
⊥平面 ;
;
(2)平面 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
试题篮
()