高中数学空间向量的应用填空题

在棱长为1的正方体ABCD﹣A₁B₁C₁D₁中，过对角线BD₁的一个平面交AA₁于E，交CC₁于F，得四边形BFD₁E，给出下列结论：
①四边形BFD₁E有可能为梯形
②四边形BFD₁E有可能为菱形
③四边形BFD₁E在底面ABCD内的投影一定是正方形
④四边形BFD₁E有可能垂直于平面BB₁D₁D
⑤四边形BFD₁E面积的最小值为
其中正确的是　     （请写出所有正确结论的序号）

三棱锥中，若，是该三棱锥外部(不含表面)的一点，给出下列四个命题，
① 存在无数个点，使；
② 存在唯一点，使四面体为正三棱锥；
③ 存在无数个点，使；
④ 存在唯一点，使四面体有三个面为直角三角形.
其中正确命题的序号是       .

已知是两条不同的直线，是两个不同的平面，有下列五个命题
①　②
③　④
⑤
其中真命题的序号是__________________________（把所有真命题的序号都填上）

在正方体中，点为正方形 的中心.下列说法正确的是     （写出你认为正确的所有命题的序号）.
①直线与平面所成角的正切值为；
②若,分别是正方形 , 的中心，则；
③若,分别是正方形 , 的中心，则；
④平面中不存在使成立的点.

给定下列四个命题：
①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；
②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；
③垂直于同一直线的两条直线相互平行；
④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是                。

如图，是的直径，垂直于所在的平面，是圆周上不同于的任意一点，则图中直角三角形有        个.（要求：只需填直角三角形的个数，不需要具体指出三角形名称）.

在正方形中，是的中点，是侧面内的动点且//平面，则与平面所成角的正切值得取值范围为                 .

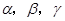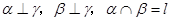下列命题：①已知平面满足则.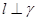
②E，F，G，H是空间四边形ABCD各边AB，BC，CD，DA的中点，若对角线BD=2，AC=4，则
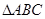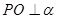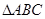③过所在平面外一点P，作，垂足为O，连接PA，PB，PC，若，则点O是的垂心
其中正确命题的序号是           。

如图，四棱锥P-ABCD中，底面为菱形，且，．

（Ⅰ）求证：；
（Ⅱ）若，求二面角的余弦值．

如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是                 ．

如图所示，在四边形中，,将四边形沿对角线折成四面体，使平面平面，则下列结论正确的是          ．

（1）；
（2）；
（3）与平面所成的角为；   
（4）四面体的体积为．

设l是一条直线，α，β，γ是不同的平面，则在下列命题中，假命题是________．
①如果α⊥β，那么α内一定存在直线平行于β
②如果α不垂直于β，那么α内一定不存在直线垂直于β
③如果α⊥γ，β⊥γ，α∩β＝l，那么l⊥γ
④如果α⊥β，l与α，β都相交，那么l与α，β所成的角互余

如图，在三棱锥中，是等边三角形，.

（1）证明:：；
（2）证明：；
（3）若，且平面平面，求三棱锥体积.

在类比此性质，如下图，在四面体P－ABC中，若PA、PB、PC两两垂直，底面ABC上的高为h，则得到的正确结论为__________________________．

如图所示，在三棱柱中，底面,是上一动点，则的最小值是       ．