高中数学正交试验设计方法解答题

现有三种基本电子模块，电流能通过的概率都是P，电流能否通过各模块相互独立.已知中至少有一个能通过电流的概率为0.999.现由该电子模块组装成某预警系统M(如图所示），针对系统M而言，只要有电流通过该系统就能正常工作.

(1)求P值
(II)求预警系统M正常工作的概率

设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为各人是否需使用设备相互独立.
（1）求同一工作日至少3人需使用设备的概率；
（2）表示同一工作日需使用设备的人数，求的数学期望.

江西某品牌豆腐食品是经过、、三道工序加工而成的，、、工序的产品合格率分别为、、．已知每道工序的加工都相互独立，三道工序加工的产品都为合格时产品为一等品；恰有两次合格为二等品；其它的为废品，不进入市场．
（1）生产一袋豆腐食品，求产品为废品的概率；
（2）生产一袋豆腐食品，设为三道加工工序中产品合格的工序数，求的分布列和数学期望．

(本题分12分）
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同．
（Ⅰ）若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;
（Ⅱ）若抽取后不放回,设抽完红球所需的次数为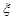,求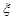的分布列及期望．

（本小题满分12分）
已知射手甲射击一次，击中目标的概率是．
（1）求甲射击5次，恰有3次击中目标的概率；
（2）假设甲连续2次未击中目标，则停止其射击，求甲恰好射击5次后，被停止射击的概率．

两个人射击，甲射击一次中靶概率是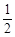，乙射击一次中靶概率是，
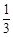（Ⅰ）两人各射击一次，中靶至少一次就算完成目标，则完成目标概率是多少？
（Ⅱ）两人各射击2次，中靶至少3次就算完成目标，则完成目标的概率是多少？
（Ⅲ）两人各射击5次，是否有99％的把握断定他们至少中靶一次？

2010年世博会于5月1日在中国上海隆重开幕，甲、乙、丙三人打算利用周六去游览，由于时间有限，三人商定在已圈定的10个国家馆中各自随机选择一个国家馆游览（选择每个国家馆的可能性相同）．
（Ⅰ）求甲、乙、丙三人同时游览同一个国家馆的概率；
（Ⅱ）求甲、乙、丙三人中至少有两人同时游览同一个国家馆的概率.

为考察某种药物预防禽流感的效果，进行动物家禽试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本.
（1）根据所给样本数据完成下面2×2列联表；
（2）请问能有多大把握认为药物有效？

	不得禽流感	得禽流感	总计
服药
不服药
总计

 

在乒乓球比赛中，甲与乙以“五局三胜”制进行比赛，根据以往比赛情况，甲在每一局胜乙的概率均为 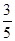．已知比赛中，乙先赢了第一局，求：
(Ⅰ)甲在这种情况下取胜的概率；
(Ⅱ)设比赛局数为X，求X的分布列及数学期望（均用分数作答）。

（本小题满分12分）某厂生产的产品在出厂前都要做质量检测，每一件一等品都能通过
检测，每一件二等品通过检测的概率为.现有10件产品，其中6件是一等品，4件是二等
品.
(Ⅰ) 随机选取1件产品，求能够通过检测的概率；
(Ⅱ) 随机选取3件产品，其中一等品的件数记为，求的分布列；
(Ⅲ) 随机选取3件产品，求这三件产品都不能通过检测的概率.

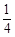甲、乙两人独立地破译1个密码，他们能译出密码的概率分别为和，求
（1）恰有1人译出密码的概率；
（2）若达到译出密码的概率为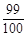，至少需要多少乙这样的人．

已知一个口袋中装有个红球（且）和个白球，从中有放回地连续摸三次，每次摸出两个球，若两个球颜色不同则为中奖，否则不中奖．
（1）当时，设三次摸球中（每次摸球后放回）中奖的次数为，求的分布列；
（2）记三次摸球中（每次摸球后放回）恰有两次中奖的概率为，当取多少时，最大．

一射击测试每人射击二次，甲每击中目标一次记10分，没有击中记0分，每次击中目标的概率为；乙每击中目标一次记20分，没有击中记0分，每次击中目标的概率为.
（Ⅰ）求甲得10分的概率；
（Ⅱ）求甲乙两人得分相同的概率.

现有甲乙丙丁四人依次抽奖，抽后放回，另一个人再抽，求至少有两人获奖的概率.

）某篮球队与其他6支篮球队依次进行6场比赛，每场均决出胜负，设这支篮球队与其他篮球队比赛胜场的事件是独立的，并且胜场的概率是.
（1）求这支篮球队首次胜场前已经负了两场的概率；
（2）求这支篮球队在6场比赛中恰好胜了3场的概率；
（3）求这支篮球队在6场比赛中胜场数的期望和方差.