(本小题满分14分)
设圆满足条件:(1)截y轴所得的弦长为2;(2)被x轴分成两段弧,其弧长的比为3︰1;(3)圆心到直线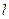 :
: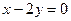 的距离为
的距离为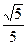 .求这个圆的方程.
.求这个圆的方程.
已知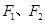 分别是双曲线
分别是双曲线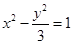 的左、右焦点,过
的左、右焦点,过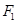 斜率为
斜率为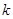 的直线
的直线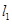 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于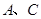 两点,过
两点,过 且与
且与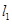 垂直的直线
垂直的直线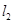 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于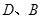 两点。
两点。
(1)求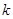 的取值范围;
的取值范围;
求四边形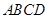 面积的最小值。
面积的最小值。
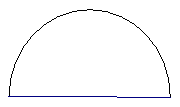
建立适当的坐标系,用坐标法解决下列问题:
已知隧道的截面是半径为4m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7m,高为3m的货车能不能驶入这个隧道?
 |
在直角坐标系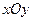 中,点
中,点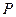 到两点
到两点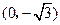 ,
,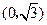 的距离之和等于
的距离之和等于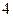 ,设点
,设点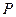 的轨迹为
的轨迹为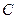 。
。
(1)求曲线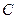 的方程;
的方程;
(2)过点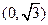 作两条互相垂直的直线
作两条互相垂直的直线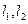 分别与曲线
分别与曲线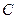 交于
交于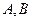 和
和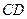 。
。
①以线段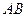 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的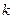 值,若不能说明理由;
值,若不能说明理由;
②求四边形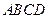 面积的取值范围。
面积的取值范围。
已知动圆过定点P(1,0),且与定直线 相切,点C在
相切,点C在 上.
上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为- 的直线与曲线M相交于A、B两点,
的直线与曲线M相交于A、B两点,
①求线段AB的长;
②问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
已知动点(x, y) 在曲线C上,将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程 ;定点M(2,1),平行于OM的直线
;定点M(2,1),平行于OM的直线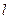 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线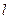 与曲线C交于A、B两个不同点.
与曲线C交于A、B两个不同点.
(1)求曲线 的方程; (2)求m的取值范围.
的方程; (2)求m的取值范围.
以直角坐标系的原点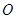 为极点,
为极点,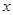 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点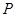 的直角坐标为
的直角坐标为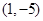 ,点
,点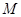 的极坐标为
的极坐标为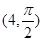 ,若直线
,若直线 过点
过点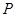 ,且倾斜角为
,且倾斜角为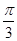 ,圆
,圆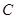 以
以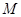 为 圆心、
为 圆心、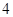 为半径。
为半径。
(I) 写出直线 的参数方程和圆
的参数方程和圆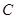 的极坐标方程;
的极坐标方程;
(Ⅱ)试判定直线 和圆
和圆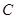 的位置关系。
的位置关系。
(本小题满分14分)
已知点 、
、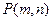 ,(
,( )是曲线C上的两点,点
)是曲线C上的两点,点 、
、 关于
关于 轴对称,直线
轴对称,直线 、
、 分别交
分别交 轴于点
轴于点 和点
和点 ,
,
(Ⅰ)用 、
、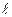 、
、 、
、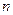 分别表示
分别表示 和
和 ;
;
(Ⅱ)某同学发现,当曲线C的方程为: 时,
时,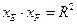 是一个定值与点
是一个定值与点 、
、 、
、 的位置无关;请你试探究当曲线C的方程为:
的位置无关;请你试探究当曲线C的方程为: 时,
时, 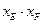 的值是否也与点M、N、P的位置无关;
的值是否也与点M、N、P的位置无关;
(Ⅲ)类比(Ⅱ)的探究过程,当曲线C的方程为 时,探究
时,探究 与
与 经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
已知椭圆 的离心率为
的离心率为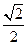 ,
,
直线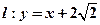 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆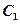 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。
(Ⅰ)求椭圆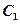 的方程;
的方程;
(Ⅱ)设椭圆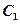 的左焦点为F1,右焦点为F2,直线
的左焦点为F1,右焦点为F2,直线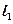 过点F1,且垂直于椭圆的长轴,动直
过点F1,且垂直于椭圆的长轴,动直
线 垂直
垂直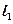 于点P,线段PF2的垂直平分线交
于点P,线段PF2的垂直平分线交 于点M,求点M的轨迹C2的方程;
于点M,求点M的轨迹C2的方程;
(Ⅲ)若AC、BD为椭圆C1的两条相互垂直的弦,垂足为右焦点F2,求四边形ABCD的面积
的最小值.
试题篮
()