如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且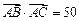 .
.
(1)求sin∠BAD的值;
(2)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求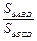 的值.
的值.
 |
已知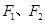 分别是双曲线
分别是双曲线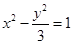 的左、右焦点,过
的左、右焦点,过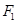 斜率为
斜率为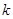 的直线
的直线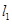 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于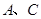 两点,过
两点,过 且与
且与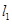 垂直的直线
垂直的直线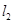 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于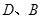 两点。
两点。
(1)求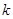 的取值范围;
的取值范围;
求四边形 面积的最小值。
面积的最小值。
已知曲线 ,给出下列四个命题:①曲线
,给出下列四个命题:①曲线 与两坐标轴围 成的图形面积不大于
与两坐标轴围 成的图形面积不大于 ;②曲线
;②曲线 上的点到原点的距离的最小值为
上的点到原点的距离的最小值为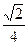 ;
;
③曲线 关于点(
关于点( ,
, )中心对称;④当x≠0,1时,曲线
)中心对称;④当x≠0,1时,曲线 上所有点处的切线斜率为负值.正确的是____________.
上所有点处的切线斜率为负值.正确的是____________.
抛物线C的方程为 ,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足
,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足 .
.
(Ⅰ)求抛物线C的焦点坐标和准线方程;
(Ⅱ)设直线AB上一点M,满足 ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上;
(Ⅲ)当 =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标 的取值范围.
的取值范围.
如图,一条螺旋线是用以下方法画成:ΔABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别以A、B、C为圆心,AC、BA1、CA2为半径画的弧,曲线CA1A2A3称为螺旋线旋转一圈.然后又以A为圆心AA3为半径画弧,这样画到第n圈,则所得螺旋线的长度 _____________.(用π表示即可)
_____________.(用π表示即可)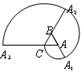
以直角坐标系的原点 为极点,
为极点,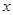 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点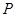 的直角坐标为
的直角坐标为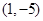 ,点
,点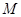 的极坐标为
的极坐标为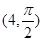 ,若直线
,若直线 过点
过点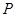 ,且倾斜角为
,且倾斜角为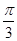 ,圆
,圆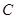 以
以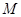 为 圆心、
为 圆心、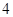 为半径。
为半径。
(I) 写出直线 的参数方程和圆
的参数方程和圆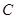 的极坐标方程;
的极坐标方程;
(Ⅱ)试判定直线 和圆
和圆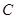 的位置关系。
的位置关系。
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线 ,将
,将 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、2倍后得到曲线
、2倍后得到曲线 . 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
. 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线 .
.
(Ⅰ)试写出直线 的直角坐标方程和曲线
的直角坐标方程和曲线 的参数方程;
的参数方程;
(Ⅱ)在曲线 上求一点P,使点P到直线
上求一点P,使点P到直线 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
(本小题满分10分)选修4-1:几何证明选讲
如图所示,AB是⊙O的直径,
G为AB延长线上的一点,GCD是⊙O的割线,过点
G作AB的垂线,交AC的延长线于点E,交AD的延
长线于点F,过G作⊙O的切线,切点为H .
求证:(Ⅰ)C,D,F,E四点共圆;
(Ⅱ)GH2=GE·GF.
试题篮
()