高中数学二次剩余试题

设函数，若 

（1）求函数的解析式；
（2）画出函数的图象，并说出函数的单调区间；
（3）若，求相应的值.

已知函数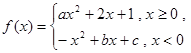是偶函数，直线与函数的图像自左至右依次交于四个不同点、、、，若，则实数的值为________．

在自然条件下，某草原上野兔第n年年初的数量记为x_n,该年的增长量y_n和 x_n与的乘积成正比，比例系数为，其中m是与n无关的常数，且x₁<m，
(1)证明：;
(2)用 x_n表示x_n+1;并证明草原上的野兔总数量恒小于m.

经市场调查，某种商品在过去50天的销售量和价格均为销售时间t（天）的函数，且销售量近似地满足f（t）＝－2t＋200（1≤t≤50，t∈N）．前30天价格为g（t）＝t＋30（1≤t≤30，t∈N），后20天价格为g（t）＝45（31≤t≤50，t∈N）．
（1）写出该种商品的日销售额S与时间t的函数关系；
（2）求日销售额S的最大值．

关于函数y= log(x-2x+3)有以下4个结论:其中正确的有            .
① 定义域为(- ;     ② 递增区间为;
③ 最小值为1;                   ④ 图象恒在轴的上方.

已知函数
(1)若函数在的单调递减区间（—∞,2],求函数在区间[3,5]上的最大值.
(2)若函数在在单区间（—∞,2]上是单调递减,求函数的最大值.

（本小题满分15分）
已知二次函数满足条件：
①当时，，且；
②当时，；
③在R上的最小值为0
（1）求的解析式；
（2）求最大的m(m>1)，使得存在，只要，就有.

函数的值域为           .

本小题满分10分
已知二次函数（其中）.
(1)若函数为偶函数，求的值；
(2)当为偶函数时，若函数，指出在上单调性情况，并证明之.

已知函数（其中）的图象如下面右图所示，则函数的图象是（     ）


A．            B．       C．       D．

已知，，若，，若，则实数和满足的一个关系式是      ，的最小值为      ．

直线，当此直线在轴的截距和最小时，实数的值是（  ）

A．1

B．

C．2

D．3

（本小题满分14分）某公司生产的新产品的成本是2元/件，售价是3元/件，
年销售量为10万件，为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是（万元）时，产品的销售量将是原销售量的倍，且是的二次函数，它们的关系如下表：

	···	1	2	···	5	···
	···	1.5	1.8	···	1.5	···

 
（2）求与的函数关系式；
（3）如果利润=销售总额成本费广告费，试写出年利润S（万元）与广告费（万元）的函数关系式；并求出当广告费为多少万元时，年利润S最大.

（本小题满分12分）
设，当时，对应值的集合为.
（1）求的值；（2）若，求该函数的最值.

已知函数（）．
（1）若的定义域和值域均是，求实数的值；
（2）若对任意的，，总有，求实数的取值范围．