高中数学第二数学归纳法试题

用数学归纳法证明不等式成立，其的初始值至少应为 (      )

A．7

B．8

C．9

D．10

用数学归纳法证明（）时，从“n=”到“n=”的证明，左边需增添的代数式是___________. 

用数学归纳法证明1＋＋＋…＋(,)，在验证成立时，左式是____．

证明：．

已知数列{a_n}满足a₁＝2，a_n＋1＝ (n∈N^*)，则a₃＝________，a₁·a₂·a₃·…·a₂₀₁₄＝________.

用数学归纳法证明1＋2＋3＋…＋n²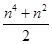＝，则当n＝k＋1时左端应在n＝k的基础上加上(　　)

A．k^2＋1

B．(k＋1)^2

C．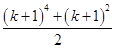

D．(k^2＋1)＋(k^2＋2)＋…＋(k＋1)^2

若f(n)＝1²＋2²＋3²＋…＋(2n)²，则f(k＋1)与f(k)的递推关系式是________．

在数列{a_n}中，a_n＝1－＋－＋…＋－，则a_k＋1等于(　　)

A．ak＋	B．ak＋－
C．ak＋	D．ak＋－

平面内有n条直线，最多可将平面分成f(n)个区域，则f(n)的表达式为(　　)

A．n＋1	B．2n
C．	D．n^2＋n＋1

某个命题与自然数n有关，若n＝k(k∈N^*)时命题成立，那么可推得当n＝k＋1时该命题也成立，现已知n＝5时，该命题不成立，那么可以推得(　　)

A．n＝6时该命题不成立	B．n＝6时该命题成立
C．n＝4时该命题不成立	D．n＝4时该命题成立

用数学归纳法证明1＋2＋3＋…＋(2n＋1)＝(n＋1)(2n＋1)时，从n＝k到n＝k＋1，左边需增添的代数式是(　　)

A．2k＋2	B．2k＋3
C．2k＋1	D．(2k＋2)＋(2k＋3)

用数学归纳法证明1＋＋＋…＋> (n∈N^*)成立，其初始值至少应取(　　)

A．7

B．8

C．9

D．10

利用数学归纳法证明不等式1＋＋＋ <f(n)　(n≥2，)的过程中，由n＝k变到n＝k＋1时，左边增加了(　 　)

A．1项

B．k项

C．项

D．项

在数列{}中，，且，
（1）求的值；
（2）猜测数列{}的通项公式，并用数学归纳法证明。

航空母舰“辽宁舰”将进行一次编队配置科学实验，要求2艘攻击型核潜艇一前一后，2艘驱逐舰和2艘护卫舰分列左、右，同侧不能都是同种舰艇，则舰艇分配方案的方法数为________．(用数字作答)