在数列 中,已知
中,已知 ,
, ,
, (
( ,
, ).
).
(1)当 ,
, 时,分别求
时,分别求 的值,判断
的值,判断 是否为定值,并给出证明;
是否为定值,并给出证明;
(2)求出所有的正整数 ,使得
,使得 为完全平方数.
为完全平方数.
(本小题满分13分)已知数列 中,
中,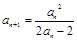 ,
,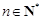 .
.
(Ⅰ)若 ,设
,设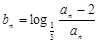 ,求证数列
,求证数列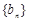 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,
,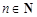 ,证明:
,证明: .
.
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…,(-1) ,即当
,即当 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
设函数f(x)=x-xlnx,数列{an}满足0<a1<1,an+1=f(an).求证:
(1)函数f(x)在区间(0,1)是增函数;
(2)an<an+1<1.
已知f(n)=1+ n∈N),g(n)=2(
n∈N),g(n)=2( -1)(n∈N).
-1)(n∈N).
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
已知数列{an}满足a1=1,且4an+1-anan+1+2an=9(n∈N).
(1)求a2,a3,a4的值;
(2)由(1)猜想{an}的通项公式,并给出证明.
已知 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项 ,
, 的部分项
的部分项 、
、 、 、
、 、 恰为等比数列,且
恰为等比数列,且 ,
, ,
, .
.
(1)求数列 的通项公式
的通项公式 (用
(用 表示);
表示);
(2)设数列 的前
的前 项和为
项和为 , 求证:
, 求证: (
( 是正整数
是正整数
平面内有n(n∈N+,n≥2)条直线,其中任何两条不平行,任何三条不过
同一点,证明:交点的个数f(n)= .
.
已知函数f(x)= x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较
x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较 +
+ +
+ +…+
+…+ 与1的大小,并说明理由.
与1的大小,并说明理由.
已知函数
(Ⅰ)若函数 在其定义域上为单调函数,求
在其定义域上为单调函数,求 的取值范围;
的取值范围;
(Ⅱ)若函数 的图像在
的图像在 处的切线的斜率为0,
处的切线的斜率为0, ,已知
,已知 求证:
求证:
(Ⅲ)在(2)的条件下,试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
试题篮
()