高中数学第二数学归纳法试题

用数学归纳法证明：
．

在数列中，，且成等差数列，成等比数列.
(1)求；
(2)根据计算结果，猜想的通项公式，并用数学归纳法证明．

在数列中，已知，且。
（1）用数学归纳法证明：；
（2）求证．

设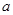是一个自然数，是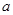的各位数字的平方和，定义数列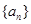：是自然数，（，）．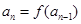
（1）求，；
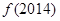（2）若，求证：；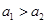
（3）求证：存在，使得．

（本小题满分14分）
已知函数f(x)=x－ax + (a－1)，．
（I）讨论函数的单调性；
（II）若，数列满足．
（1）  若首项，证明数列为递增数列；
（2）  若首项为正整数，数列递增，求首项的最小值．

已知，，．
（1）当时，试比较与的大小关系；
（2）猜想与的大小关系，并给出证明．

已知，是函数的两个零点，其中常数，，设．
（Ⅰ）用，表示，；
（Ⅱ）求证：；
（Ⅲ）求证：对任意的．

记的展开式中，的系数为，的系数为,其中
(1)求（2）是否存在常数p,q(p<q),使，对，恒成立？证明你的结论.

各项均为正数的数列对一切均满足．证明：
（1）；
（2）．

在中，不等式成立；在凸四边形ABCD中，
不等式成立；在凸五边形ABCDE中，不等式成立，，依此类推，在凸n边形中，不等式__    ___成立.

已知数列中，，且．为数列的前项和，且．
（1）求数列的通项公式；
（2）设，求数列的前项的和；
（3）证明对一切，有．

设数列{}满足：a₁=2，对一切正整数n，都有
(1)探讨数列{}是否为等比数列，并说明理由；
(2)设

已知数列{b_n}是等差数列，b₁＝1，b₁＋b₂＋…＋b₁₀＝145.
(1)求数列{b_n}的通项公式b_n；
(2)设数列{a_n}的通项a_n＝log_a(其中a＞0且a≠1)．记S_n是数列{a_n}的前n项和，试比较S_n与log_ab_n＋1的大小，并证明你的结论.

是否存在常数a,b使等式对于一切n∈N*都成立？若存在，求出a,b的值，若不存在，请说明理由。

用数学归纳法证明：“,在验证n＝1时，左端计算所得的项为（   ）

A．1

B．

C．

D．