高中数学第二数学归纳法试题

用数学归纳法证明（）时，从“n=”到“n=”的证明，左边需增添的代数式是___________. 

某地区为了绿化环境进行大面积植树造林，如图，在区域 内植树，第一棵
树在点A_l（0，1），第二棵树在点．B₁（l， l），第三棵树在点C₁（1,0），第四棵树在点C₂（2,0），接着按
图中箭头方向每隔一个单位种一棵树，那么
（1）第n棵树所在点坐标是（44,0），则n=            ．
（2）第2014棵树所在点的坐标是           .

已知，（其中）
（1）求及；
（2）试比较与的大小，并说明理由．

已知,,,, ,由此你猜想出第n个数为         

黑白两种颜色的正六形地面砖块按如图的规律拼成若干个图案，则第4个图案中有白色地面砖________________块.

已知,,,,…,由此你猜想出第n个数为         

用火柴棒摆“金鱼”，如图所示：

按照上面的规律，第4个“金鱼”图需要火柴棒的根数为

A．24

B．26

C．28

D．30

已知数列的前n项和为，且，令.
（1）求证：数列是等差数列，并求数列的通项公式；
（2）若，用数学归纳法证明是18的倍数．

用数学归纳法证明1＋＋＋…＋(,)，在验证成立时，左式是____．

证明：．

设实数 $c>0$，整数 $p>1,n\in N^{+}$.
（1）证明：当 $x>-1$且 $x\ne 0$时， $(1+x{)}^p>1+px$；
（2）数列 $\left\{a_n\right\}$满足 $a_1>c^{\frac{1}{p}},a_{n+1}=\frac{p-1}{p}{a}_n+\frac{c}{p}{a_n}^{1-p}$，证明： $a_n>a_{n+1}>c^{\frac{1}{p}}$.

若不等式＋＋…＋>对一切正整数n都成立，猜想正整数a的最大值，并证明结论．

已知数列{a_n}满足a₁＝2，a_n＋1＝ (n∈N^*)，则a₃＝________，a₁·a₂·a₃·…·a₂₀₁₄＝________.

用数学归纳法证明1＋2＋3＋…＋n²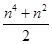＝，则当n＝k＋1时左端应在n＝k的基础上加上(　　)

A．k^2＋1

B．(k＋1)^2

C．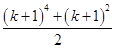

D．(k^2＋1)＋(k^2＋2)＋…＋(k＋1)^2

设数列{a_n}满足a₁＝3，a_n＋1＝a_n²－2na_n＋2，n＝1,2,3，…
(1)求a₂，a₃，a₄的值，并猜想数列{a_n}的通项公式(不需证明)；
(2)记S_n为数列{a_n}的前n项和，试求使得S_n<2ⁿ成立的最小正整数n，并给出证明．