关于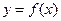 ,给出下列六个命题:(1)若
,给出下列六个命题:(1)若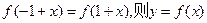 是
是
周期函数;(2)若 ,则
,则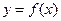 为奇函数;(3)若函数
为奇函数;(3)若函数 的
的
图象关于 对称,则
对称,则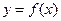 为偶函数;(4)函数
为偶函数;(4)函数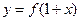 与函数
与函数 的
的
图象关于直线 对称;(5)若
对称;(5)若 ,则
,则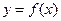 的图象关于点(1,0)
的图象关于点(1,0)
对称;(6)若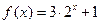 ,则
,则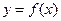 的图像可以由函数
的图像可以由函数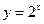 的图像仅通过平移变
的图像仅通过平移变
换得到。则所有正确命题的序号是 ___。
某射手射击1次,击中目标的概率是0.9,他连续射击4次,且各次射击是否击中目标相互之间没有影响.有下列结论:(1)他第3次击中目标的概率是0.9;(2)他恰好击中目标3次的概率是 ;(3)他至少击中目标1次的概率是
;(3)他至少击中目标1次的概率是 .
.
其中正确结论的序号是 (写出所有正确结论的 序号)
序号)
给出下列命题:
①y=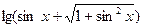 是奇函数;
是奇函数;
②若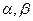 是第一象限角,且
是第一象限角,且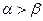 ,则
,则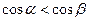 ;
;
③函数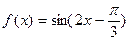 的一个对称中心是
的一个对称中心是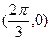 ;
;
④函数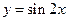 的图象向左平移
的图象向左平移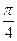 个单位,得到函数
个单位,得到函数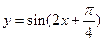 的图象,
的图象,
其中正确命题的序号是____________(把正确命题的序号都填上).
已知三个平面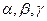 ,若
,若 ,且
,且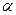 与
与 相交但不垂直,直线
相交但不垂直,直线 分别为
分别为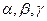 内
内
的直线,给出下列命题:
①任意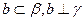 ; ②任意
; ②任意 ; ③存在
; ③存在 ;
;
④存在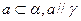 ; ⑤任意
; ⑤任意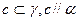 ; ⑥存在
; ⑥存在 .
.
其中真命题的序号是_________ .(把你认为正确的命题序号都填上)
给出下列命题,其中正确的命题是 (填序号).
①若平面 上的直线m与平面
上的直线m与平面 上的直线n为异面直线,直线l是
上的直线n为异面直线,直线l是 与
与 的交线,那么l至多与m,n中的一条相交;
的交线,那么l至多与m,n中的一条相交;
②若直线m与n异面,直线n与l异面,则直线m与l异面;
③一定存在平面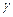 同时与异面直线m,n都平行.
同时与异面直线m,n都平行.
下列命题中:
①设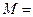 {直线},
{直线},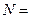 {圆},则集合
{圆},则集合 的元素个数为:0或1或2;
的元素个数为:0或1或2;
②过抛物线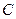 :
: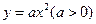 的焦点
的焦点 作直线
作直线 交抛物线
交抛物线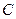 于
于 两点,则
两点,则 ;
;
③已知二面角 的平面角的大小是
的平面角的大小是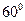 ,
,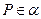 ,
,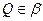 ,
, 是直线
是直线 上的
上的 任意一点,过点
任意一点,过点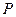 与
与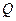 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为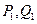 ,且
,且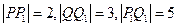 ,则
,则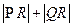 的最小值为:
的最小值为: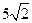 ;
;
④已知 是平面,
是平面, 是直线,若
是直线,若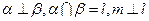 ,则
,则 ;
;
⑤已知点M是抛物线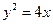 上的一点,F为抛物线的焦点,点A在圆
上的一点,F为抛物线的焦点,点A在圆 上,
上,
则 的最小值为4;
的最小值为4;
以上命题正确的为 (把所有正确的命题序号写在横线上)。
给出如下命题:
①直线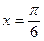 是函数
是函数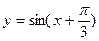 的一条对称轴;
的一条对称轴;
②函数 关于点(3,0)对称,满足
关于点(3,0)对称,满足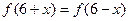 ,且当
,且当 时,函数为增函数,则
时,函数为增函数,则 在
在 上为减函数;
上为减函数;
③命题“对任意 ,方程
,方程 有实数解”的否定形式为“存在
有实数解”的否定形式为“存在 ,方程
,方程 无实数解”;
无实数解”;
④ 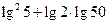

以上命题中正确的 是 .
是 .
已知l,m,n是三条不同的直线,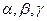 是三个不同的平面,下列命题:
是三个不同的平面,下列命题:
①若l∥m,n⊥m,则n⊥l;
②若l∥m,m α,则l∥α;
α,则l∥α;
③若l α,m
α,m β,α∥β,则l∥m;
β,α∥β,则l∥m;
④若α⊥γ,β⊥γ,α∩β=l,则l⊥γ
其中真命题是 ▲ .(写出所有真命题的序号)
.设 ,
, 为不同的两点,直线
为不同的两点,直线 ,
, ,以下命题中正确的序号为 .
,以下命题中正确的序号为 . 不论
不论 为何值,点N都不在直线
为何值,点N都不在直线 上;
上; 若
若 ,则过M,N的直线与直线
,则过M,N的直线与直线 平行;
平行; 若
若 ,则直线
,则直线 经过MN的中点;
经过MN的中点; 若
若 ,则点M、N在直线
,则点M、N在直线 的同侧且直线
的同侧且直线 与线段MN的延长线相交.
与线段MN的延长线相交.
.已知P是双曲线 的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为
的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为 ,有下列命题:
,有下列命题:
①双曲线的一条准线被它的两条渐近线所截得的线段长度为 ;
;
②若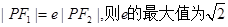 ;
;
③ 的内切圆的圆心横坐标为
的内切圆的圆心横坐标为 ;
;
④若直线PF1的斜率为
其中正确的命题的序号是 。
已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,求直线AE与平面ABC1D1所成角的正弦值 .
试题篮
()