.定义在实数集R上的函数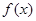 ,如果存在函数
,如果存在函数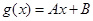 (A、B为常数),使得
(A、B为常数),使得 对一切实数
对一切实数 都成立,那么称
都成立,那么称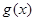 为函数
为函数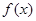 的一个承托函数。给出如下四个结论:
的一个承托函数。给出如下四个结论:
①对于给定的函数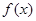 ,其承托函数可能不存在,也可能有无数个;
,其承托函数可能不存在,也可能有无数个;
②定义域和值域都是R的函数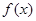 不存在承托函数;
不存在承托函数;
③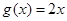 为函数
为函数 的一个承托函数;
的一个承托函数;
④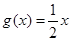 为函数
为函数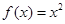 的一个承托函数。
的一个承托函数。
其中所有正确结论的序号是__________________.
给出定义:若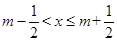 (其中
(其中 为整数),则
为整数),则 叫做离实数
叫做离实数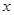 最近的整数,记作
最近的整数,记作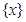 ,即
,即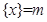 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数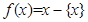 的四个命题:
的四个命题:
①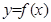 的定义域是
的定义域是 ,值域是
,值域是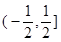 ;
;
②点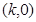 是
是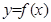 的图像的对称中心,其中
的图像的对称中心,其中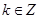 ;
;
③函数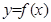 的最小正周期为
的最小正周期为 ;
;
④ 函数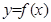 在
在 上是增函数.
上是增函数.
则上述命题中真命题的序号是 .
①由“若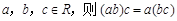 ”类比“若
”类比“若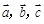 为三个向量,则
为三个向量,则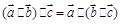 ”;②设圆
”;②设圆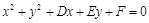 与坐标轴的4个交点分别为A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),则
与坐标轴的4个交点分别为A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),则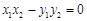 ;③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;④在实数列
;③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;④在实数列 中,已知a1 = 0,
中,已知a1 = 0, ,则
,则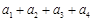 的最大值为2.上述四个推理中,得出的结论正确的是_____________(写出所有正确结论的序号).
的最大值为2.上述四个推理中,得出的结论正确的是_____________(写出所有正确结论的序号).
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p、q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列三个命题;
①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个.
②若pq=0,且p+q≠0,则“距离坐标”为(p、q)的点有且仅有2个.
③若pq≠0,则“距离坐标”为(p、q)的点有且仅有4个.上述命题中,正确命题是 (填写序号)
给出下列说法:
① 函数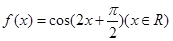 的图象关于直线
的图象关于直线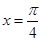 对称;
对称;
② 设函数f(x)是定义在R上的以5为周期的奇函数,若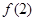 >1,
>1,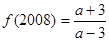 ,
,
则a的取值范围是(0,3) ;
③ 若对于任意实数x,都有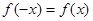 ,且
,且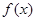 在(-∞,0]上是减函数,
在(-∞,0]上是减函数,
则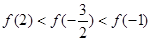 ;
;
④ 函数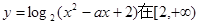 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是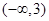 ;
;
其中说法正确的序号是 ;(填上所有正确的序号)
给出下列四个结论:
① 若角的集合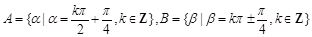 ,则
,则 ;
;
② 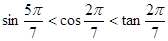
③ 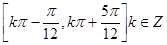 是函数
是函数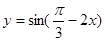 的单调递减区间
的单调递减区间
④ 函数 的周期和对称轴方程分别为
的周期和对称轴方程分别为
其中正确结论的序号是 .(请写出所有正确结论的序号)。
已知命题p:所有指数函数都是单调函数,则非p为______________.
试题篮
()